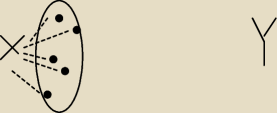graf
1: czy w każdym grafie nawet multigrafach, istnieją zawsze 2 wierzchołki o tych samych stopniach?
Widziałem dowody trywialne dla grafów prostych bo taki ma max stopień n−1 więc z Dirichleta...
ale w multigrafie może być np stopien (n−1)*2 max
6 sty 18:30
1: chyba że w zadaniu "wykaż że tak jest w każdym grafie rzędu ≥2" oznacza tylko grafy proste
6 sty 18:32
wredulus_pospolitus:
Zapewne chodzi o grafy proste.
6 sty 18:41
wredulus_pospolitus:
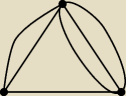
w końcu dla multigrafów masz np taki.
6 sty 18:43
wredulus_pospolitus:
dodatkowo −−− zawsze można użyć pętli.
6 sty 18:44
1: 
6 sty 18:52
1: analogiczne pytanie czy to już znów zachodzi dla każdego grafu w tym multigrafu etc zachodzi że
jeśli st. minimalny wierzchołków jest ≥ floor(n/2) to czy oznacza że graf jest spójny
6 sty 19:02
1: w dowodzie można założyć że nie jest i mamy np dwa mniejsze grafy, wtedy mamy
jakiś wierzchołek x i od niego ≥ floor(n/2) krawędzi i analogicznie y, wykładowca stwierdził
że poza x w tym kółku i po prawej analogicznie jest ≥ floor(n/2) wierzchołków ale co jeśli nasz
x jest połączony np dwoma czy trzema krawędziami z którymś, wtedy niekoniecznie tam musi być
chyab ≥ floor(n/2 wierzchołków
6 sty 19:04
1:
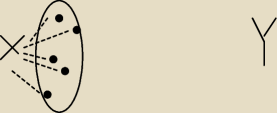
6 sty 19:04
1: chociaż dobra to ma sens plączę chyba niepotrzebnie
6 sty 19:06
1: ale no np dla n = 6, i np po lewej mamy X i 2 wierzchołki w kółku i tak samo po prawej,
i X może być połączony 3 krawędziami z każdym z dwóch i to nie oznacza że tam jest ≥ floor(n/2)
wierzchołków
co więcej po prawej tez nie ma ≥ floor(n/2) wierzch.
więc dowód się wysypie stwierdzając tak jak wyżej aczkolwiek robiąc tak jak on że n ≥
floor(n/2) + ≥ floor(n/2) + 2 # to 2 jako X i Y
6 ≥ 2 + 2 + 2 jest ok bo mamy 2 w dwóch kółkach + x i y
6 sty 19:09
1: a co dla n = 6
6 ≥ 1 + 3 + 2 ale no 1 ≥ floor(6/3) = 2 nie prawda więc chyba to jest głupotą co on zapisał
6 sty 19:10
1: ** 1≥ floor(6/2) = 3 i tak nie prawda
6 sty 19:13
wredulus_pospolitus:
W mutigrafach − w momencie gdy możesz stosować pętle możesz de facto uzyskać dowolny stopień na
każdym wierzchołku ... a co za tym idzie − nie trudno jest stworzyć niespójny multigraf .
Wszystkie te twierdzenia dotyczą grafów PROSTYCH.
Multigraf to 'wolna amerykanka'
6 sty 19:25
6 sty 19:57
 w końcu dla multigrafów masz np taki.
w końcu dla multigrafów masz np taki.