Zadanie z parametrem Nebula : Witam, mam problem z poniższym zadaniem, nie wiem co mam dalej zrobić Dla jakich wartości parametru m równanie x² + 2mx = 2x + m ma dwa różne pierwiastki mniejsze od 2? Wiem, z treści: Δ>0 , a≠0 , x1<2 , x2<2 Obliczyłem deltę: Δ = (2m−2)² + 4m 4m² − 8m + 4 + 4m m² − 1 + 1 więc wiemy z tego że m ∊ R, ponieważ nie ma miejsc zerowych. Lecz co dalej mam zrobić, nie mam pojęcia Z góry dziękuje za pomoc

chichi: jak dasz wszystko na lewą i stworzysz z tego funkcje f, to wystarcz wysunąć wierzcholek na lewo od 2 i wartość funkcji w 2 nad oś OX

Nebula : Tak to wszystko miałem na lewo i wyszło mi wtedy tak: x² + (2m−2)x − m = 0 ale nie do końca wiem co mi to daje oprócz obliczenia delty. Chodzi o zamienienie to na postać: a(x−p)+q?

chichi: nieee, po prosru f(x) = x² +(2m − 2x) − m. Δ > 0 ← 2 miejsca zerowe p < 2 ← wierzcholek na lewo, czyli jedno z m.z. juz mniejsze od 2 f(2) > 0 ← wypychasz prawie ramię nad oś OX przed 2, stad drugie m.z. wypada przed 2

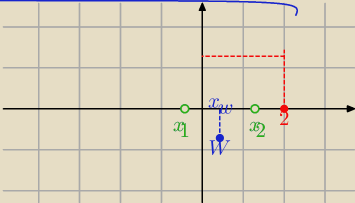
Eta: Parametr "m" spełnia układ warunków Δ>0 x_w<2 f(2)>0 teraz licz......

Nebula : Czyli w takim razie dla p<2 wychodzi: −b/2a < 2 czyli: (−2m+2)/2 < 2 m>0 a f(2) > 0 to będzie wyglądać tak: 4+4m−4−m > 0 3m > 0 m>0 czyli końcowy wynik to m∊(0;+∞) Dzięki wielkie za pomoc

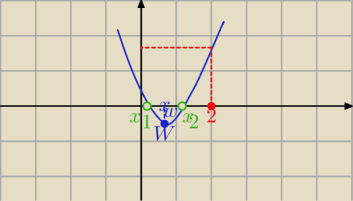
Eta: Ach ten edytor

chichi:

Nebula : O rysunek to już całkowicie rozjaśnia wszystko. Dzięki jeszcze raz