nierówność kubaaa5467: (x−2)(−x⁴ + 8x − 16) ≥ 0 jak to rozwiązać? wyszły mi trzy rozwiązania: −2, 2, −2 ale nie wiem jak narysować wykres, mógłby mi ktoś wytłumaczyć? bardzo dziękuję

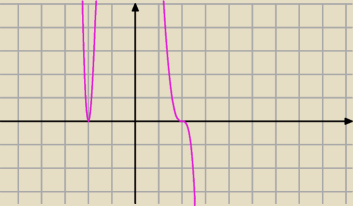
chichi: (x − 2)(−x⁴ + 8x² − 16) = (x − 2)[−(x − 2)²(x + 2)²] = −(x − 2)³(x + 2)² "węża" rysujemy od prawej strony od dołu, bo a_n < 0 (to wynika z granicy funkcji w +∞). liczba 2 jest pierwiastkiem nieparzystej krotności, więc wykres przebija 2, −2 jest pierwiastkiem parzystej krotności więc następuje odbicie od osi

kubaaa5467: A jeśli rozwiążę to metodą podstawiania t za x²? wtedy wychodzą mi t= 4 więc x=2 lub x= −2 wtedy otrzymuję wynik x= 2 z (x−2) i wyniki x=2 lub x= −2 z (−x⁴ + 8x² − 16). Czy bezpośrednio z tego można narysować wykres? delta wychodzi równa 0, więc w pierwiastku powinno być odbicie, ale nie wiem, jak to zrobić bo mam dwa pierwiastki i jeszcze 2 powtarza się dwa razy więc też powinno być odbicie mógłbym jeszcze prosić o wytłumaczenie dlaczego mój sposób jest zły? Ten sposób który mi napisałeś/aś rozumiem i bardzo dziękuję, ale w tym moim trochę się pogubiłem i zastanawiam się co robię źle

chichi: ale wtedy rysujesz wykres takiego czegoś: f(t) = −t² + 8t − 16, a u Ciebie w nierówności nie dość, ze występuje powtórnie dwumian (x − 2), to jest to funkcja zmiennej x, a nie t. ty je sztucznie podstawiłeś po to, aby rozłożyć ten wielomian z nawiasu, a nie narysować wykres

kubaaa5467: Dobra, bardzo dziękuję za pomoc