Pole powierzchni całkowitej walca markowewino: Oblicz pole powierzchni całkowitej walca o objętości 24π, w którym wysokość jest dwa razy krótsza od przekątnej przekroju osiowego

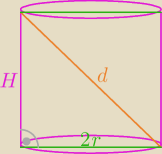
chichi: z treści mamy iż (1) πr²H = 24π oraz (2) d = 2H ponadto z tw. Pitagorasa mamy: 4r² + H² = d²

	3
no to podstawiając (2) mamy, że: 4r2 + H2 = (2H)2 ⇔ r2 =		H2
	4

	3
wracamy zatem do (1): π		H2H = 24π ⇔ ... dalej już łatwo
	4

markowewino: czy mogę prosić o dokończenie jednak pola powierzchni całkowitej? Mam obliczone r= √3*³√4 oraz h=2³√4

J23: P_c= 2πr(H+r)=.......

markowewino: mam problem w działaniach na pierwiastkach o różnych stopniach i podstawach. Proszę o pomoc w rozwiązaniu tego Ppc = 2π(√3*³√4)²+2π*√3*³√4*2³√4

J23: (√3*³√4)²= 3³√16= 3*³√8*2=3*2³√2= 6³√2 √3*³√4*2³√4= √3*2³√16=4√3*³√2

markowewino: Dziękuję, wszystko się zgadza

Eta: Na zdrowie https://pl.wikipedia.org/wiki/Jabol