dowód
klucz:
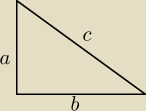
Mam wykazać ze a+b≤c
√2.
Czy taki dowód jest poprawny?
Podnoszę obie strony do kwadratu
(a+b)
2 ≤ 2c
2,
korzystam ze to trójkąt prostokątny
a
2+2ab+b
2 ≤ 2a
2+2b
2 ⇔ (a−b)
2 ≥ 0
Czy w dobrą stronę to robię?
26 gru 22:02
ABC:
zasadniczo ok , jakiś komentarz że podnoszenie do kwadratu stronami jest tu przekształceniem
równoważnym bo obie strony nierówności są dodatnie ,
na końcu komentarz że nierówność (a−b)2≥0 jest prawdziwa , więc i wyjściowa jest prawdziwa
26 gru 22:43
klucz: A nie musze jakość wyjść od a2+b2=c2 i z tej równości dowieść nierównośći a+b≤c√2.
Czy mogę zrobić tak jak zrobiłem w poście 22:02?
26 gru 23:04
Eta:
Można z nierówności między średnimi .. kwadratową i arytmetyczną
| a+b | | a2+b2 | |
| ≤√ |
| |2 i a2+b2=c2 |
| 2 | | 2 | |
(a+b)
2≤ 2(a
2+b
2)
√
a+b ≤
√2c
26 gru 23:09
Eta:
Podobne zadanie:
Wykaż,że w prostopadłościanie o krawędziach długości a,b,c,
i przekątnej d prostopadłościanu
zachodzi nierówność
a+b+c ≤√3d
teraz @
klucz pokaż ten dowód
26 gru 23:20
klucz: A czemu mam pokazywać to a+b+c ≤√3d
Jeszcze raz ponwaiam pytanie :
Czy musze jakość wyjść od a
2+b
2=c
2 i z tej równości dowieść nierównośći a+b≤c√2.
Czy mogę zrobić tak jak zrobiłem w poście 22:02?
26 gru 23:27
ABC:
klucz możesz wyjść z a2+b2=c2 , to zasadniczo jeden pies, wtedy robisz tak
mnożysz obustronnie przez 2
2a2+2b2=2c2
teraz korzystasz z tego że 2ab≤a2+b2 co wynika z (a−b)2≥0
a więc możesz napisać
a2+2ab+b2≤2a2+2b2=2c2
z przechodniości masz a2+2ab+b2≤2c2 i teraz ponieważ a,b,c >0 to pierwiastkujesz stronami
bo możesz i otrzymujesz
a+b≤√2c (nie musisz pisać wartości bezwzględnych)
26 gru 23:32
ABC:
możesz tak jak o 22:02 napisałem ci zasadniczo ok , ch....ego masz nauczyciela/nauczycielkę
26 gru 23:34
klucz: a skad ten komentarz "możesz tak jak o 22:02 napisałem ci zasadniczo ok , ch....ego masz
nauczyciela/nauczycielkę
27 gru 08:15
ABC:
bo skoro masz takie wątpliwości to słaby twój nauczyciel że ci nie wytłumaczył
27 gru 08:33
klucz: Moze tobie lepiej tumaczą
27 gru 08:37