geometria gdańskie wyd. oświatowe FX447: Niech punkt S będzie środkiem ciężkości trójkąta KLM. Uzasadnij że suma kwadratów odległości punktu S od wierzchołków trojkąta jest 3 razy mniejsza od sumy kwadratów długości boków trójkąta KLM

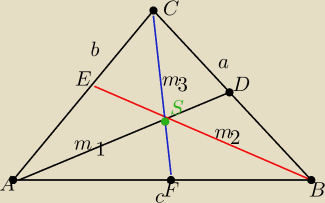
Klasa V-VIII: Może mozna prościej i pewnie bedzie można m₁= 0,5√2(b²+c²)−a² m₂= 0,5√2(c²+a²)−b² m₃= 0,5√2(a²+b²)−c² Wyprowadzic sobie mozna z twierdzenia cosinusów

	2
|AS|=		m1
	3

	2
|BS|=		m2
	3

	2
|CS|=		m3
	3

a²+b²+c²> 3(|AS|²+|BS|²+|CS|²)

ABC: małolat dobrze zaczynałeś ale nie to było do pokazania ale z tego co napisałeś wynika po prostych przekształceniach

	4		1
		(m12+m22+m32)=		(a2+b2+c2)
	9		3

czyli to co trzeba

as: Dobrze żarło i........... zdechło

Klasa V-VIII: Witam Już widzę . I tam ma byc ΔKLM a nie ABC . Ale to nie powinno stanowić problemu

ABC: zawsze trzeba być czujnym tu parę zadań wyżej jest wątek o okręgu opisanym na trójkącie równoramiennym, gdzie nikt nie napisał że oprócz rozwiązania b=√80 jest jeszcze drugie b=√20 ale ty tam się wycofałeś z dyskusji więc jesteś usprawiedliwiony

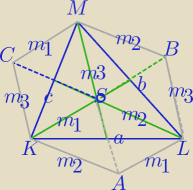Mila: 1) Równoległobok KALS: |AS|=m₃ a²+m₃²=2m₁²+2m₂² analogicznie dla pozostałych równoległoboków b²+m₁²=2m₂²+2m₃² c²+m₂²=2m₁²+2m₃² ====================(+) a²+b²+c²=2m₁²+2m₂²−m₃²+2m₂²+2m₃²−m₁²+2m₁²+2m₃²−2m₂²⇔ a²+b²+c²=3m₁²+3m₂²+3m₃²

	1
m12+m22+m32=		(a2+b2+c2)
	3

============================

Mila: W trzeciej linijce od dołu ma być na końcu prawej strony : −m₂²

ABC: tożsamość równoległoboku − ważna własność charakteryzująca normy pochodzące od iloczynu skalarnego

Mila: Miłego świętowania.