22 gru 21:32
świruś: pomóż ktoś
22 gru 23:14
świruś: pls
22 gru 23:38
wredulus_pospolitus:
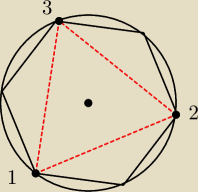
Najpierw przedstawię 'zredukowaną' sytuację, czyli sześciokąt foremny.
Zauważ, że zaznaczony trójkąt równoboczny zliczamy aż trzykrotnie (czyli o dwa razy za dużo).
Ponieważ robimy to dla każdego przypadku gdy prosta 'k' przechodzi przez wierzchołek 1,
wierzchołek 2 i wierzchołek 3.
Jest tu także drugi analogiczny trójkąt równoboczny, który oczywiście także jest zliczany
3−krotnie.
A skąd wiemy, że w 99kącie foremnym będą takie trójkąty równoboczne istniały (bo nie w każdym
wielokącie foremnym je mieć będziemy)?
| | 99 | | 6 | |
Ponieważ mamy |
| = 33 <−−− jest to liczba całkowita (a patrząc na rysunek mamy |
| |
| | 3 | | 3 | |
= 2).
Dodatkowo to podaje nam ile takich trójkątów mamy.
Mam nadzieję, że rozumiesz o co chodzi.
23 gru 05:16
Świruś: Dlaczego dzieląc na trzy mamy liczbę trójkątów równobocznych? To z czegoś jeszcze wynika?
23 gru 10:47
Świruś: Jednak rozumiem dzieki narysowałam sobie parę przykładów jak takie trójkąty równoboczne
wyglądają w wielokątach foremnych i już wiem
23 gru 10:54
Świruś:
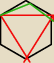
Po prostu liczbę boków dzieli się na trzy żeby jakby podzielić na trzy równe części boki tej
figury, że jeden bok trójkąta idzie przy dwóch bokach sześciokąta itd...
23 gru 10:56
Świruś: A jak się nie da podzielić to nie będzie trójkąta w środku tak?
23 gru 10:57
wredulus_pospolitus:
10:56 −−− taaak
no jak się nie da podzielić na '3 równe części' .
| | 8 | | 1 | |
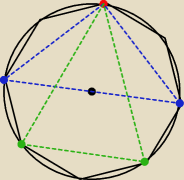
A jak się nie da ... to popatrz na przykładzie ośmiokąta: |
| = 2 |
| |
| | 3 | | 3 | |
więc jak z
czerwonego wyjdziemy i połączymy
niebieskie wierzchołki to nie będzie to
trójkąt równoboczny bo podstawa jest za długa (pomiędzy wierzchołkami u podstawy masz '3
wierzchołki wielokąta' podczas gdy przy ramionach masz tylko '1 wierzchołek wielokąta'
a przy wersji połączenia
zielonych masz '1 wierzchołek' wielokąta u podstawy a po dwa na
bokach.
Nie wiem czy dobrze to wyjaśniłem
23 gru 13:38
wredulus_pospolitus:
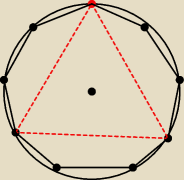
podczas przy 9−cio kącie (na rysunku "prawie"
) foremnym da się zrobić taki trójkąt ...
| | 9 | |
łącząc co trzeci wierzchołek (a wiemy to z |
| = 3) |
| | 3 | |
23 gru 13:41
wredulus_pospolitus:
analogicznie −−− wybierając wierzchołki z wielomianu o n−wierzchołkach będziemy w stanie
zbudować:
| | n | |
a) kwadrat −> jeżeli |
| jest liczbą całkowitą |
| | 4 | |
| | n | |
b) pięciokąt −> jeżeli |
| jest liczbą całkowitą |
| | 5 | |
itd.
bo tylko wtedy możemy brać " co k'ty " wierzchołek tak aby wybrać ich dokładnie tyle ile chcemy
(np. 4 dla kwadratu) i 'wrócimy' do wierzchołka z którego rozpoczynaliśmy wybór.
23 gru 13:49
Świruś:
23 gru 15:04