I OMG 2005 świruś: W przestrzeni danych jest takich n punktów (n≥4), że żadne cztery nie leżą na jednej płaszczyźnie. Każde dwa z tych punktów połączono odcinkiem niebieskim lub czerwonym. Udowodnij, że można tak wybrać jeden z tych kolorów, aby każde dwa punkty były połączone odcinkiem lub łamaną wybranego koloru. Wyjaśni mi ktoś polecenie? o co w tym zadaniu w ogóle chodzi? i jak zrobić to zadanie

. : Mamy przestrzeń. W przestrzeni mamy n punktów, takich że dowolna prosta przechodząca przez dwa punkty może zawierać co najwyżej jeszcze jeden punkt. Masz wykazać że jeżeli wybierzesz sobie kolor (czerwony lub niebieski) to droga w takim właśnie kolorze jesteś w stanie się dostać z każdego jednego punktu do drugiego.

świruś: a dasz jakiś szkic rozwiązania?

świruś: czyli możemy użyć tylko jednego koloru?

świruś: przecież to oczywiste, że tak się da (chyba, że czegos nadal nie rozumiem)

świruś: czyli ta łamana może składać się maks. z dwóch odcinków?

. : Poczekaj. Wrócę do domu. Jak tam wyniki z pierwszego etapu?

świruś: bardzo dobre wyniki

świruś: bo ja tutaj nie rozumiem jak to działa, jak ta łamana wygląda i jak mamy łączyć te punkty z płaszczyzn

świruś: a łamana może łączyć np. 4 punkty?

wredulus_pospolitus: pod pojęciem łamanej chodzi o dowolną drogę (niekoniecznie bezpośrednią) np. z punktu A do B, później z B do C ... itd. aż w końcu do Z a nie tylko bezpośrednio z A do Z.

świruś: błagam wredulus napisz mi rozwiązanie

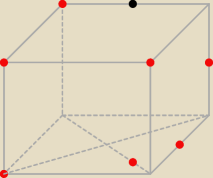
wredulus_pospolitus: tu masz przykładowe rozmieszczenie n=8 punktów tak, maksymalnie 3 były na jednej płaszczyźnie. Zauważ, że np. ten punkt nie może być umiejscowiony jako 9 punkt, ponieważ wtedy na płaszczyźnie zawierającą górną ścianę tego graniastosłupa będziemy mieli 4 punkty.

wredulus_pospolitus: i teraz zadanie mówi −−− że każdy punkt z każdym łączysz odcinkiem i tenże odcinek kolorujesz na jeden kolor (powiedzmy że w losowy sposób) −−− niebieski lub czerwony. Mamy dowieść, że dla DOWOLNEGO pokolorowania tych odcinków, możemy sobie spojrzeć na to i powiedzieć: "wybieram czerwony" lub "wybieram niebieski" (my decydujemy jedną z tych opcji). A następnie jesteśmy w stanie z każdego punktu przejść do każdego innego (niekoniecznie bezpośrednio) poruszając się JEDYNIE po odcinkach w tymże właśnie przez nas kolorze.

świruś: mogę rozwiązanie takie gotowe? jeśli to nie problem wredulusie

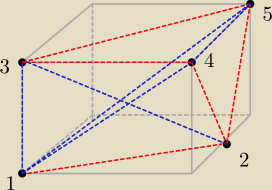
wredulus_pospolitus: To jest PRZYKŁADOWE pokolorowanie dla n=5 punktów. (i już jest to słabo widoczne). I zadaniu mówią nam, że jak widzimy coś takiego, że patrzymy sobie na to i mówimy Wybieram kolor (jak sobie wybiorę) niebieski i prawdą ma być, że z każdego punktu przejdę do każdego tylko po niebieskich odcinkach, no to piszemy: 1 −> 3 −> 2 1 −> 3 1 −> 4 1 −> 5 2 −> 3 2 −> 3 −> 1 −> 4 2 −> 3 −> 1 −> 5 3 −> 1 −> 4 3 −> 1 −> 5 4 −> 5 no i oczywiście 'powrotna droga' analogiczna ... w efekcie wypisałem jak mogę się dostać z każdego punktu do każdego korzystając tylko z niebieskich odcinków. Ty teraz postaraj się wypisać drogi korzystając JEDYNIE z czerwonych odcinków.

wredulus_pospolitus: Najpierw musisz zrozumieć jaka jest idea tego co masz wykazać

świruś: a jeśli wszystkie odcinki pomaluję na niebiesko i będę chciała się przedostać czerwonym to co?

wredulus_pospolitus: Miałaś indukcję matematyczną Chodzi mi o sposób rozumowania ... bo on tutaj będzie 'jak znalazł'

świruś: 1>2 1>2>4>3 1>2>4 1>2>5

świruś: no dobra to rozumiem, to jak to wykazać?

wredulus_pospolitus: oto chodzi ... Ty przed przechodzeniem podejmujesz decyzję co do koloru i chodzi oto, że masz wykazać, że MOŻESZ podjąć decyzję co do koloru tak że są możliwe te przejścia. Innymi słowy −−− że nie będzie sytuacji, że co by nie było, to nie ma sytuacji, że zarówno po niebieskich droga nie dostaniesz się do wszystkich punktów jak również poruszając się po czerwonych drogach nie dostaniesz się do wszystkich punktów. Więc jakbyś miała wszystkie na niebiesko drogi ... to po prostu wybierasz niebieski kolor Jeżeli masz jeden punkt który jest połączony z wszystkimi innymi tym samym kolorem −−− wybranie tegoż koloru załatwia sprawę

wredulus_pospolitus: zrobiłaś drogi tylko '1' ... powinnaś jeszcze drogi z początkiem w innych punktach zrobić ... ale mam nadzieję, że już rozumiesz ideę 'czym jest łamana' tutaj

świruś: tak tak tak (zrozumienie polecenia jest w tym zadaniu najtrudniejsze ale jak wykazać to zadanie jak to udowodnić, że zawsze będzie taka możliwość, że będą drogi do wszystkich punktów w jednym kolorze

wredulus_pospolitus: ponownie się pytam −−− czy miałaś indukcję matematyczną ... czy rozumiesz ideę takiego właśnie dowodzenia

świruś: nie widziałam tego niestety

świruś: znaczy robiłam czasami jakieś zadania w takim stylu indukcji, ale nie znam jakiś reguł

wredulus_pospolitus: dobra ... to bardzo szybko podam ideę indukcji matematycznej. Dowód poprzez indukcję matematyczną polega na wykazaniu, że JEŻELI coś jest prawdą dla n elementów to wtedy wtedy będzie to także prawdą dla n + 1 elementów. Dowodząc jeszcze, że jest to prawdą dla najmniejszego n = 4 (w naszym przypadku), daje nam dowód na to, że jest to prawda dla dowolnego n ≥ 4. Bo: 1. wykazaliśmy prawdę dla n = 4 2. skoro wiemy, że jeżeli jest prawdą dla n to jest też dla n+1 ... to skoro wykazaliśmy prawdę dla n=4 to wiemy że i dla n=5 będzie prawdą 3. skoro prawdą jest dla n=5 to też będzie prawdą dla n=6 .. itd .. w efekcie wykazaliśmy, że jest prawdą dla DOWOLNEGO n≥4.

świruś: i to już koniec?

wredulus_pospolitus: Jak to rozumowanie zastosować w naszym zadaniu. Zastanówmy się przez moment ... powiedzmy, że jest to prawdą dla jakiegoś 'n' punktów. Że jakkolwiek byśmy drogi nie pokolorowali, to możemy wybrać jeden kolor także że z każdego punktu do każdego przejdziemy po jednym kolorze. Teraz jak wygląda sytuacja dla 'n+1' punktów? Po prostu dorzucamy nowy punkt, i tenże punkt łączymy z wszystkimi dotychczasowymi punktami i połączenia te kolorujemy. Mamy więc trzy sytuacje jakie mogą zajść: 1. Wszystkie odcinki do tego nowego punktu są w kolorze który dla wersji 'n punktów' był wybrany. 2. Mamy różnego koloru odcinki łączące ten nowy punkt z pozostałymi. 3. Wszystkie odcinki do tego nowego punktu są w innym kolorze niż ten który był wybrany dla wersji 'n punktów'.

wredulus_pospolitus: tak −−− to był koniec IDEI dowodu poprzez indukcję

wredulus_pospolitus: I teraz: w przypadku 1 −−− sprawa prosta ... miałaś już wszystkie drogi pomiędzy 'n' punktami ... natomiast do 'n+1' punktu dostaniesz się BEZPOŚREDNIO z tych 'n' punktów (bo te wszystkie odcinki do nowego punktu są w naszym 'wybranym' kolorze). a jak wygląda sytuacja w 2 przypadku

świruś: to też się da, bo skoro da się pomiędzy tymi n punktami się przemieszczać, które były na początku to można dostać się przez inne punkty do nowego punktu jeśli mamy różne kolory nowych odcinków, bo to oznacza, że na pewno znajdzie się taki kolor jaki już wybraliśmy do tych n punktów

wredulus_pospolitus: tak ... a zapisując to innymi słowy. jeżeli pomiędzy 'starym' punktem a nowym, jest ten 'wybrany kolor' to mamy bezpośrednie połączenie, a jeżeli nie ... to wiemy że z tego 'starego punktu' możemy przejść do DOWOLNEGO 'starego punktu', więc także do takiego który ma 'dobrą drogę' do nowego punktu. okey ... a co w przypadku 3 Gdzie (przykładowo) mieliśmy dla n punktów wybrany kolor niebieski ... a nowy punkt połączony jest z każdym za pomocą czerwonego koloru

świruś: wtedy trzeba zmienić kolor i dostawać się za pomocą tego nowego punktu do reszty punktów

wredulus_pospolitus: czyli ten nowy punkt (może być) będzie 'hubem' dla każdego starego punktu aby się dostać do każdego starego punktu. To wyczerpuje nam możliwości. W efekcie wykazaliśmy, że jeżeli tylko jest to prawdą dla jakiegoś 'n' ... to będzie to prawdą także dla 'n+1' (i w konsekwencji także dla n+2, n+3, itd.) Więc pozostaje nam wykazać to dla n = 4

wredulus_pospolitus: I to możemy zrobić na dwa sposoby ... wykazać to bezpośrednio (trochę zabawy może z tym być) albo wykazać się 'sprytnym−lenistwem'

świruś: nie wiem jak

świruś: się wykazać tym sprytnym lenistwem

wredulus_pospolitus: sprytne−letnistwo −−− wskazówka: wiemy, już że jak dla 'n' jest spełnione to jest spełnione dla n+1 ... no to zamiast udowadniać dla n=4 ... to może wykażemy to dla n=3 (tak tak ... w zadaniu mamy, że n≥4 ale to niczemu nie przeszkadza). Jedyna kwestia −−− to to, że mają podane że żadne 4 punkty nie leżą na jednej płaszczyźnie (na dobrą sprawę, nie wiem po co to założenie). Jednak to dla samego dowodu nie ma znaczenia. A jakbyśmy chcieli jeszcze bardziej 'po bandzie' pójść to zamiast udowadniać dla n=3, to byśmy udowodnili dla n = 2 co jest 'automatycznie' prawdą bo w końcu wtedy mamy tylko jeden odcinek

wredulus_pospolitus: jak dla mnie ... oni celowo 'utrudnili' to zadanie (wyobrażenie go), poprzez: 1. warunek o braku 4 punktów na jednej płaszczyźnie (a nie ma warunku o tym, że 3 nie mogą być współinowe, więc przyjmują że połączenie dwóch punktów nie musi być odcinkiem, a np. łukiem) 2. wrzucili punkty w przestrzeń (mniej osób jest wstanie sobie to wyobrazić) niż gdyby to było na płaszczyźnie.

wredulus_pospolitus: 3. warunek że n ≥ 4 a nie n ≥ 2. Przy n ≥ 2 istniałaby większa szansa, że konkursowicze zaczną od wariantu n=2 i z niego przechodząc do n=3 szybko załapią 'przejście rekurencyjne' czyli to wykazanie które robiliśmy z 'n' do 'n+1'

wredulus_pospolitus: Więc ... zauważ, że gdyby było n≥2 ... to bez problemu byś udowodniła to, że dla n=2 jest to spełnione, prawda Baaa ... nawet dla n=3 nie jest to raptem parę rysunków.

wredulus_pospolitus: Lub jedno zdanie uzasadniające.

wredulus_pospolitus: Kończąc −−− mam nadzieję, że "czujesz" to rozwiązanie które zasugerowałem i teraz wygląda ono rozsądnie i stosunkowo łatwe ... najtrudniejszą częścią zadania tak naprawdę było zrozumienie o co im chodzi A przy okazji −−− mam nadzieję, że załapałaś ideę dowodu 'przez indukcję matematyczną' i jak będziesz miała to na zajęcia lub gdzieś indziej to będziesz rozumiała DLACZEGO TAK WYGLĄDAJĄ kolejne kroki indukcji i dlaczego jest to dowód.

świruś: dziękuję

. : I co... Nie takie straszne to zadanie, nieprawdaż?!

świruś: o co tu chodzi czy to ta sama osoba pisze?

świruś: czy to pisze ta sama osoba?

. : Tak... Ja to wredulus jeno z komórki

świruś: aha