Oblicz dł. ramion trójkąta równoramiennego o podstawie 8, jeśli opisano na nim o Monika: Od czego zacząć? Oblicz dł. ramion trójkąta równoramiennego o podstawie 8, jeśli opisano na nim okrąg o promieniu 5

Monika: To znaczy tego zadania nie da się obliczyć?

chichi: porównaj wzory na pole trójkąta

	abc		a + b + c
P =		= √p(p−a)(p−b)(p−c), gdzie p =		.
	4R		2

Natura:

	a
R=
	2sinβ

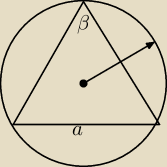
sinβ= Masz kąt i dumaj dalej ja musze wyjechac

Monika: Natura, i wyszedł mi sin beta = 8/10 Pola trójkąta przyrównałam, ten wzór z sinusem i ten z R, ale doszłam do tego, że wyszło mi a=8 które już miałam jako dane. I znów jestem w otchłani.

Mila: Rozwiąż wg wskazówki chichi.

an: @ dalej obliczasz cosinus β i z tw. cosinusów b=√80

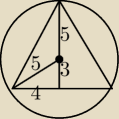
an: albo II sposób Pitagoras

Natura: Więc dalej skoro sinβ=0,8 to β=54^o

	1800−54o
Stad miara kąta przy podstawie trójkata to		= 63o
	2

Więc dalej

b		a
	=
sin63o		sin 54o

	sin63o*a
b=
	sin54o

	0,891*8
b≈		≈8,91
	0,8

Tutaj trzeba korzystac albo z kalkulatora albo z tablic

Monika: An, Twój sposób jest najprostszy ten z 21.12. godz. 17:13. a) ten odcinek, który Ci wyszedł x=3 wyliczam z Pitagorasa w tym małym trójkącie b) obliczam h trójkąta równoramiennego jako x+R= 3+5=8 c) z połówki trójkąta równoramiennego, z tw. Pitagorasa, mając połowę podstawy =4 oraz wys. trójkąta =8 wyliczam długość ramienia. Uff, długo będę pamiętać to zadanie Dziękuję Wszystkim za wsparcie i życzę Wam pogodnych w sercu i na niebie Świąt oraz pomyślnego Nowego 2024 Roku Niech nam się darzy