Przyprostokątne trójkąta prostokątnego mają 8 i 6. Poprowadzono Monika: Męczy mnie to zad. i nie wiem, jak go ruszyć. Proszę pomóżcie Przyprostokątne trójkąta prostokątnego mają 8 i 6. Wyznaczono dwusieczne kątów ostrych. Oblicz długość odcinków tych dwusiecznych.

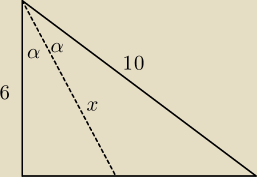wredulus_pospolitus: metoda I (dla mnie najszybsza)

	1+cos(2α)
cos(2α) = 2cos2α − 1 −−−> cos2a =
	2

a więc:

62		6   1 +   10		16		4
	=		=		=
x2		2		20		5

	5*36
−−−> x2 =		= 45 −−−> x = √45 = 3√5
	4

analogicznie dla drugiego kąta

Monika: Bardzo Ci dziękuję

an: dla kątów ostrych trójkąta prostokątnego c=√a²+b² ax/2 sinα+xc/2 sinα=ab/2 ⇒

	ab
xsinα=		; xcosα=a mnożymy stronami
	a+c

	2a2b
x2sin2α=
	a+c

	b
sin2α=		dzielimy stronami
	c

	2a2c
x2=
	a+√a2+b2

	2c
x= a√(		)
	a+c

	2*10
x1= 6√(		) =3√5
	6+10

	2*10		8
x2= 8(		) =		√10
	8+10		3

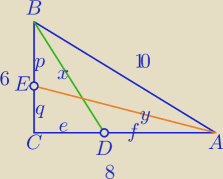Mila: 1) z tw. o dwusiecznej:

e		6
	=		i e+f=8
f		10

	3
10e=6f⇔e=		f
	5

8
	f=8⇔ f=5, e=3
5

2) W ΔBCD: x²=6²+3² x=√45, d=3√5 3x

p		10		5
	=		=		⇔4p=5q
q		8		4

5		8
	q+q=6 ⇔q=
4		3

	8
w ΔACE: y2=(		)2+82
	3

	8
y=		√10
	3

=======

Monika: An i Mila − bardzo Wam dziękuję