proszę o rozwiązanie anna: dwa boki deltoidu mają długość 2√3 a pozostałe dwa mają długość 3√4 + 2√2 wiedząc że kąt deltoidu leżącego między dwoma dłuższymi bokami ma miarę 45⁰ Oblicz miarę kąta deltoidu leżącego między dwoma krótszymi bokami

anna: zadanie zostało rozwiązane

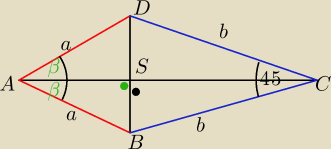
Natura: a=AB=2√3 b=BC=3√4+2√2 W ΔSBC

	SB|
sin22,5o=
	|BC|

|SB|=|BC|*sin22,5^o

	1−cos45o
sin22,5o= √
	2

	√2−√2
sin22,5o=
	2

	√2−√2
|SB|=3*√4+2√2*		=3(po prostych obliczeniach ,nie są aż tak zmudne jakby to na
	2

początku sie wydawało W ΔASB

	SB|
sinβ=
	|AB|

	3		√3		√3
sinβ=		*		=		β=60o
	2√3		√3		2

więc 2β=120^o Kąt miedzy dwoma krótszymi bokami wynosi 120^o Zadanie to można tez rozwiązac bez korzystania ze wzoru połowkowego 1) najpierw w ΔDCB z twierdzenia cosinusow obliczyc dłogośc boku |DB| 2) znowu z twierdzenia cosinusow obliczyc kąt miedzy dwoma krótszymi bokami Czasami trzeba sie zmierzyc z trudnymi obliczeniami

Mila: Nie ma trudnych rachunków w drugim sposobie |DB|=6

Natura: dzień dobry Milu

Mila: Witam miło

an: Kłania się twierdzenie sinusów