zadanie z przystawania trójkątów Paradygmaty: W trójkącie ABC punkty D, E leżą odpowiednio na odcinkach AC i BC tak, że AE i BD są odpowiednio dwusiecznymi kątów CAB i ABC. Niech P, Q będą odpowiednio rzutami punktu C na proste BD i AE. Udowodnić, że PQ jest równoległy do AB.

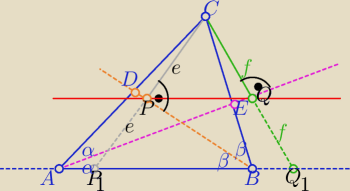
Eta: Dwusieczne BD i AE są symetralnymi odpowiednio kątów ABC i CAB zatem punkt P₁ jest symetryczny do C względem P i leży na prostej AB i analogicznie punkt Q₁ leży na prostej AB to odcinek PQ jest środkową ΔP₁Q₁C więc PQ || P₁Q₁ || AB c.n.w.