zadanie z przystawania trójkątów Paradygmaty: Rozważmy prostokąt ABCD i punkt P znajdujący się na boku AB. Niech F, G będą rzutami P odpowiednio na przekątne BD i AC. Wykaż, że suma PG + PF jest stała, niezależnie od wyboru P (na boku AB).

an:

	ab
x+y=
	√a2+b2

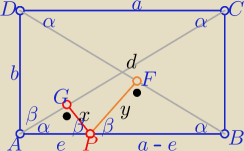
Eta: Z podobieństwa trójkątów APG , PFG i ACD z cechy (kkk)

x		b		eb		y		b		ab−eb
	=		⇒ x=		i		=		⇒ y=
e		d		d		a−e		d		d

|AC|=|BD|=d= √a²+b²

	ab
x+y=		−−− suma stała i nie jest zależna od wyboru punktu P na boku AB
	√a2+b2

Mila: ΔPFB