Funkcja kwadratowa Haniulaa (again;p): Wyznacz wzór funkcji kwadratowej f w postaci iloczynowej wiedząc, że prosta o równaniu y=90 przecina wykres tej funkcji w punktach o odciętych −5 oraz −1, zaś największa wartość tej funkcji jest równa 98. Mam nadzieję, że wam nie zawracam głowy, aczkolwiek niektóre zadania z przedmiotów ścisłych ciężko mi wchodzą

wredulus_pospolitus: jest to bardzo podobne zadanie, więc tym razem chce interakcji z Twej strony

wredulus_pospolitus: 1. Co nam daje informacja, że NAJWIĘKSZA wartość tejże funkcji to +98

Haniulaa (again;p): No to się wkopałam To co na pewno wiem: 98 to q dla wierzchołka, jednoczesnie funkcja ma ramiona skierowane do dołu, wiec a<0 Nie jestem w stanie jednak zrozumieć, w jaki sposób ta prosta przecina te punkty. Może to w ogóle nie jest sprawa wizualizacji tylko trzeba to jakoś obliczyć... może x=−5 y=90, tak samo z −1, ale czy to coś mi da?

ABC: jakbyś się uparł to brute force układ równań f(x)=ax²+bx+c f(−5)=90 f(−1)=90 f(−3)=98 90=25a−5b+c 90=a−b+c 98=9a−3b+c a=−2 b=−12 c=80 −2x²−12x+80= −2(x²+6x−40)=−2(x+10)(x−4)

wredulus_pospolitus: pierwsze zadanie −−− i dokładnie o taką odpowiedź mi chodziło prosta y = 90 jest to prosta RÓWNOLEGŁA do osi OX (czyli równoległa do prostej y=0) co za tym idzie, wiemy że f(−5) = f(−1) = 90 Pamiętasz ... w tamtym zadaniu powiedziałem Ci jak można wyznaczyć x_wierzchołka znając miejsca zerowe funkcji kwadratowej. Ta reguła działa dla dowolnych takich x_a i x_b takich, że f(x_a) = f(x_b) i dokładnie z tego tutaj mamy skorzystać ... związku z tym ile wynosi x_wierzchołka (czy tam 'p') I jak będzie wyglądała ta funkcja (jeszcze NIE w postaci iloczynowej)

wredulus_pospolitus: @ABC −−− nie psuj zabawy ... to raz ... a dwa −−− nie wyjaśniłeś skąd wiesz ze x_wierzchołka = −3 ... ale nie psuj zabawy

ABC: skąd ja to wiem ... olśnienie z wyższych wymiarów rzeczywistości

wredulus_pospolitus: Na pewno całkę iteracyjną pyknąłeś i stąd to wiesz.

ABC: dobra idę sprawdzać wzory skróconego mnożenia i logarytmy, 60 klasówek do sprawdzenia, masz wolną rękę

Jolanta: X₁ i x₂ to uszy człowieka a broda to wierzchołek ( przy a > 0) albo czubek głowy to wierzchołek (przy a<O) PPrzy założeniu że twarz jest symetrycznie zbudowana

aa:

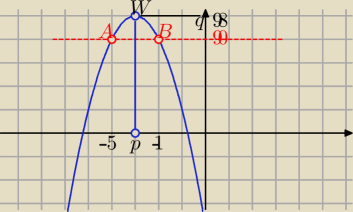
	−5−1
xw=p=		= −3 ; yw=q= 98
	2

f(x)= a(x+3)²+98 i B(−1,90) a=.... = −2

. : No i nie pozwolą się młodej wykazać... ech...

aa: Idź :: na

Haniulaa (again;p): @wredulus_pospolitus Myslalam ze zasada z wyliczaniem sredniej x tyczy sie tylko miejsc zerowych. Jednak skoro tyczy sie generalnie x to nawet lepiej (mam nadzieje ze dobrze to rozumiem) Więc wiemy że W(−3,98) mogę probowac wyliczac a, pozniej funkcję w postaci kanonicznej ale to chyba nie ta droga.

Jolanta: Ja tylko niosę pomoc😉

Jolanta: Parabola jest symetryczna tam gdzie wierzchołek jest od symetrii

wredulus_pospolitus: Haniu −−− a jak ci wyszło to −3.98

wredulus_pospolitus: to będzie właśnie ta droga 1. wyznaczasz y_wierzchołka 2. wyznaczasz x_wierzchołka 3. zapisujesz w postaci 'wierzchołkowej' 4. podstawiasz jedną z wartości funkcji podane w treści zadania 5, masz wyznaczoną wartość współczynnika 'a'. 6. albo wymnażasz, Δ i postać iloczynowa ... ALBO ... 0 = f(x) i wyznaczasz miejsca zerowe i piszesz postać iloczynową

Haniulaa (again;p): @Jolanta Kurcze, jakoś nic mi to nie mówi:( tzn. wiem ze parabola jest symetryczna tam gdzie jest wierzcholek ale w tym przypadku.. no nie wiem

aa: a= −2 f(x)=−2(x+3)²+98 f(x)= −2[(x+3)²−49] f(x)= −2(x+3+7)(x+3−7) f(x)= −2(x+10)(x−4) ================

Jolanta: To była uwaga do tego obliczania wierzcholka

Haniulaa (again;p): Hmm.. chyba najbardziej rozsądny będzie z mojej strony powrót tutaj jutro, na dziś dam sobie spokój, zważywszy też na to że wszystko zaczęło mi się mieszać Ale dziękuję za pomoc, doceniam.

Jolanta: Układ równań można zrobic

Jolanta: f_x=ax²+bx+c dla x=−1 i x =−5. y=90. Dla x=−3. y=98 90=a−b+c

	−b		−b
90=25a−5b+c z wzoru xw=		−3=		. b=6a
	2a		2a

Podstawiasz. b

Jolanta: Oj sypnelam się w drugim podstawiamy x = −3 y=98