Styczna Karolek12: Znalezc rowna stycznych do krzywej (x+1)²+(y−1)²=4 Prostopadlych do prostej 4x−3y−1=0 Styczna bedzie miec rownanie y=−3/4x+b Wstawiam w miejsce y i wychodzi mi rownanie ale wynik zły Czy jest to wgl dobry sposob? Jak nie to jak to zrobic najlepiej bez pochodnych

chichi: masz równanie prostej w postaci ogólnej k: 3x + 4y − 4b = 0 środek S = (−1,1), no to masz: d(S,k) = r, tu korzystam ze wzoru na odległość punktu od prostej P.S. twój sposób powinien wypluć te same styczne, pewnie błąd rachunkowy

Karolek12: Skąd u ciebie wzielo sie k: 3x+4y−4b=0?

6latek:

	3
y=−		x+b
	4

	3
y+		x−b=0 /*(4)
	4

4y+3x−4b=0

6latek:

	4		1
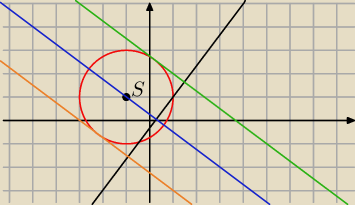
Czarna y=		x−		ta jest dana
	3		3

	3
Niebieska y−1=−		(x+1) prostopadła do czarnej
	4

	3		3		3		1
y=−		x−		+1=−		x+
	4		4		4		4

	3		1
y+		x−		=0
	4		4

3x+4y−1=0 postac ogólna więc A=3 B=4 C=−1

	|C−C1|
d=		i d=2 odległośc dwóch prostych równoległych
	√A2+B2

|−1−C1|
	=2
5

|−1−C₁|=10 −1−C₁=10 −C₁= 11 C₁=−11 lub −1−C₁=−10 C₁=9 Styczne będa miały takie równania 3x+4y−11=0 (zielona lub 3x+4y+9=0 (pomarańczowa Zrobienie na poczatek rysunku znacznie ulatwia sprawe według mnie

ABC: Małolat rozwijasz się .. u mnie w szkole uczy pan który ma 73 lata, może pójdziesz w jego ślady

6latek: Dobry wieczór ABC Ten Pan to jeszcze stary wychów