wolfram picasssoo: https://www.wolframalpha.com/input/?i=arccot+x czemu arcctg pokazuje jako taka dziwna funkcje? Chcialem sprawdzic nierownosc ale jest jakas dziwna funkcja z przerwa w zerze

6latek: funkcja y=arcctg(x) jest funkcją odwrotną do funkcji y=ctg(x) Stąd jest zapisana jako y=ctg⁻¹(x)

picasssoo: no tak ale czemu zle pokazuje wykres funkcji?

6latek: A to powinno byc znane Funkcja f(x)=ctg(x) zredukowana do przedziału otwartego (0,π) tzn funkcja g= f_|(0,π)}| jako wzajemnie jednoznaczne odwzorowanie przedziału (0,π) na zbiór ℛ ma funkcję odwrotną Funkcje odwrotna do g oznaczymy tak g⁻¹= arcctg(x) : g⁻¹:ℛ→(0,π) i czytamy arcus cotangens (x)

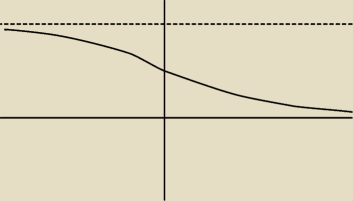
picasssoo: czy funkcja nie powinna byc taka?

b.: Tak to zwykle wygląda, chociaż w zasadzie jest kwestią umowy, jak zawężamy dziedzinę ctg, żeby wziąć z niego funkcję odwrotną. Zwykle rzeczywiście jest to (0,π) i w sumie pierwszy raz widzę, żeby ktoś brał taką definicję jak na wolframalpha.

picasso: a czy arcctg(x−7) < π/2 to (−7; ∞) ?