Funkcja kwadratowa po angielsku
arturex:
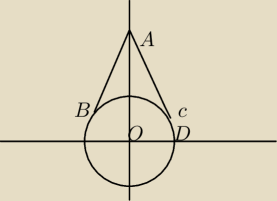
Rysunek do zadania 6.
Siemka mam problem z zadaniami z funkcji kwadratowej po angielsku. Podstawa jest troszkę inna i
nie wszystko dobrze rozumiem i nie wiem jak rozwiązać. Może wam uda się mi pomóc.
1.Points A and B have coordinates (5, 2) and (10, −1) respectively. Find the equation of the
perpendicular bisector of AB
b) Find the equation of the circle with centre A which passes through B.
2.The function f is defined by f(x) = −2x
3 − 8x − 13 for x <−3.
a) Express f(x) in the form −2(x + a)
2+ b, where a and b are integers.
b)Find the range off f
c)Find an expression for f
−1(x).
3.The curve with equation y=x
2−2x−5 is translated by (−3na górze 1 na dole)
a) Find the equation of the translated curve, giving your answer in the form y=ax
2+bx+c
b) The curve with equation y=x
2−2x−5 is transfomed to a curve with equation y= 4x
2−4x−5
describe fully the single transformation that has been applied.
4.The function f is defined as follows:
f(x)=licznik(x
2−9)/mianownik(x
2+9) for x >3
a) find an expression for f
−1(x)
b) Show that 1 − licznik18/mianownik(x
2+9) can be expressed as licznik(x
2−9)/mianownik(x
2+9)
and hence state the range of f
c) Explain why the composite function ff cannot be performed
5. The equation of a circle is x
2+ y
2 + ax + by− 12= 0. The points A (3, −1) and B (4, 6) lie
on the circle.
a)Find the values of a and b and hence find the coordinates of the centre of the circle.
b)Find an equation of the tangent to the circle at the point A, giving your answer in the form
px + qy =k, where p, qand k are integers.
6.The diagram shows the circle with equation x
2 + y
2 = 20. Tangents touching the circle at
points B and C pass
through the point A (0, 10). The point D is where the circle crosses the positive x−axis.
a)By letting the equation of a tangent be y = mx + 10, find the two possible values of m.
b)Find the coordinates of B, C and D.
x2+(mx+10)2=20 i skoro szukasz stycznych, to równanie ma mieć jedno rozwiązanie
przekształcasz , liczysz deltę itd