Pole czworokąta
Uczeń: Z wierzchołka C trójkąta równobocznego ABC o boku długości 1 poprowadzono dwie półproste, które
podzieliły kąt ACB na trzy równe części. Z wierzchołka A poprowadzono wysokość, która wraz z
tymi półprostymi i bokiem AB ogranicza pewien czoworokąt. Oblicz jego pole. Wynik podaj z
dokładnością do części setnych.
7 gru 22:39
an:
P=3/4tg10o−1/8(tg40o−tg20o)≈0,07285406⇒ =0,07
8 gru 09:31
Uczeń: A czy mógłbym prosić o rozpisanie tego, skąd to się wzięło?
10 gru 19:30
an: Trochę zaangażowania. zrób rysunek.
10 gru 19:52
Eta:
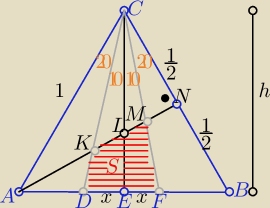
S −− szukane pole
| | 1 | | 1 | | 1 | |
P1= PMNC = |
| *|MN|*|CN| = |
| tg20o , bo |MN|= |
| *tg20o |
| | 2 | | 8 | | 2 | |
| | 1 | | 1 | | 1 | |
P2= PKNC = |
| *|KN|*|NC| = |
| *tg40o , bo |MN|= |
| *tg40o |
| | 2 | | 8 | | 2 | |
| | 1 | |
P3= PKMC = P2−P1= |
| (tg40o−tg20o) |
| | 8 | |
| | 1 | | 3 | | √3 | |
P4= PDFC |
| *2x*h = h2*tg10o = |
| *tg10o , bo x= h*tg10o i h= |
| |
| | 2 | | 4 | | 2 | |
S= P
4− P
3
| | 3 | | 1 | |
S= |
| tg10o− |
| (tg40 o−tg20 o) ( jak podał an  |
| | 4 | | 8 | |
=====================
10 gru 20:44
Eta:
| | 1 | |
W trzeciej linijce wkradł się chochlik ............ ma być: bo |KN|= |
| *tg40o |
| | 2 | |
10 gru 20:48
Uczeń: Bardzo dziękuję za pomoc, wyjaśnienie i rozpisanie tego!
10 gru 21:45