równanie darling: Do czego dązą pierwiastki x₁ i x₂ równania kwadratowego ax² + bx + c = 0 gdy a dąży do zera b i c są stałe oraz b ≠ 0

ABC: użyj alternatywnych wzorów na pierwiastki równania kwadratowego , których używają numerycy gdy b² jest dużo większe niż 4ac

darling: co masz na mysli?

ABC: wzory które znam z książki o ZX Spectrum z lat młodości

	2c
x1,2=
	−b±√b2−4ac

tu dobrze widać że gdy a→0 to jeden pierwiastek idzie do U−{c}{b} a drugi do nieskończoności

Jolanta:

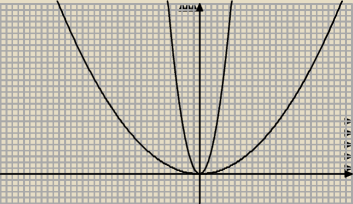
	1
Ten wąski wykres to y=x2. Ten szeroki to y =		x2
	20

Czym mniejsze a tym ramiona będą bliżej osi x Jezeli wzór będzie taki jak podajesz to parabola Będzie przecinała os x w dwóch punktach czymniejsze będzie a tym bardziej będą od siebie oddalone Czyli jeden x będzie dążył domu minus nieskonczonosci a drugi do plus nieskończoności

darling: ad abc tylko ja w zyciu na zajeciach nie widzialem takiego wzoru i takie troche nielegalne wydaje sie uzycie gp ad jolanta rozumiem o co chodzi ale to takie wytlumaczenie graficzne i nie wiem czy to trzeba jakos zapisac wynioskowac czy co

ABC: na jakich studiach jesteś ? na politechnice to legalny wzór , zresztą łatwo go wyprowadzić

darling: analityka gospodarcza

wredulus_pospolitus: To coś z katedry ekonomii i zarządzania Bo dla mnie pierwsze skojarzenie to 'fikuśne' nazwanie ekonomii

ABC:

	c
ze wzorów Viete'a masz x1*x2=		podstawiając na x2 zwykły wzór dostajesz:
	a

	c		1		c		2a
x1=		*		=		*		i a się skraca
	a		x2		a		−b+√b2−4ac

darling: katedra jest metod ilosciowych w naukach spolecznych troche cos mniej ogolnego niz ekonomia bo skupia sie na ekonometrii analizie danych itp

darling: chociaz poki co jest troche sporo matematyki w porownaniu do tych innych ekonomicznych kierunkow takich bardziej typowych