Przedziały
adam : | | 1 | |
A = {x∊R : cos4 x ≤ |
| } |
| | 16 | |
B = { x∊R ∃ t∊R t
2 + xt +1>0}
Czy A to cos ≤0.5
x ∊( π/3 +2kπ ; 5π/3 + 2kπ)
I jak zrobić b?
3 gru 22:18
ite:
A ← do poprawienia, warunek cos(x) ≤ 0,5 nie jest dobry, sprawdź dla x = π
B ← warunek t2+xt+1>0
przekształcamy do postaci xt+t2+1>0
ta nierówność liniowa jest prawdziwa gdy t=0
wtedy warunek jest spełniony dla każdego x∊ℛ
4 gru 15:11
adam: A w jakim sensie dla π? A to jak nalezy to rozwiazac
4 gru 15:14
adam: B a jak to policzylas/es
4 gru 15:15
ite:
π należy do podanego przedziału (π/3 +2kπ ; 5π/3 + 2kπ) − gdy k=1
i cos(π) = −1
więc cos
4(π) = 1 a to więcej niż 1/16
czyli rozwiązanie z 22:18 nie jest poprawne
A jak można to rozwiązać?
dalej zastosuj dwukrotnie wzór na różnicę kwadratów
4 gru 15:34
ite: w pierwszej linijce miało być k=0
4 gru 15:35
adam: (cosx − 0.5)(cosx + 0.5)(cos(x)2 + 0.25) ≤ 0
4 gru 15:59
ite:
żeby sobie ułatwić rozwiazywanie 15:59 można wprowadzić zmienną pomocniczą t∊[−1;1]
(t− 0.5)(t + 0.5)(t
2 + 0.25) ≤ 0
ostatni czynnik przyjmuje tylko wartości dodatnie
więc rozwiązaniem będzie
−0.5 ≤ t ≤ 0.5
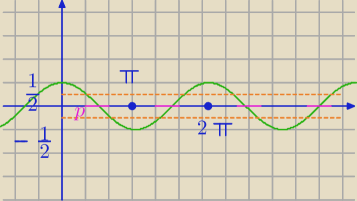
teraz wracamy do −0.5 ≤ cos(x) ≤ 0.5
ten warunek spełniają wartości zaznaczone na wykresie na różowo
czy to jest jasne?
4 gru 16:36
 żeby sobie ułatwić rozwiazywanie 15:59 można wprowadzić zmienną pomocniczą t∊[−1;1]
(t− 0.5)(t + 0.5)(t2 + 0.25) ≤ 0
ostatni czynnik przyjmuje tylko wartości dodatnie
więc rozwiązaniem będzie
−0.5 ≤ t ≤ 0.5
teraz wracamy do −0.5 ≤ cos(x) ≤ 0.5
ten warunek spełniają wartości zaznaczone na wykresie na różowo
czy to jest jasne?
żeby sobie ułatwić rozwiazywanie 15:59 można wprowadzić zmienną pomocniczą t∊[−1;1]
(t− 0.5)(t + 0.5)(t2 + 0.25) ≤ 0
ostatni czynnik przyjmuje tylko wartości dodatnie
więc rozwiązaniem będzie
−0.5 ≤ t ≤ 0.5
teraz wracamy do −0.5 ≤ cos(x) ≤ 0.5
ten warunek spełniają wartości zaznaczone na wykresie na różowo
czy to jest jasne?