przedziały klaudiusz: B y∊(π/4 ;π/2) U (3π/2 ; 7π/4) A x∊(−∞ ; −8) U (−6; ∞) Jak wyznaczyć A X B oraz czy B X A to co innego?

. : A X B to będą pary (x, y). W takiej kolejnosci B X A to będą pary (y, x). W takiej kolejnosci Wiec jak wtedy będą wyglądały te zbiory?

klaudiusz: A×B=(−∞,−8)×(π/4,π/2)∪(−∞,−8)×(3π/2,7π/4)∪(−6,∞)×(π/4,π/2)∪(−6,∞)×(3π/2,7π/4) B×A=(π/4,π/2)×(−∞,−8)∪(π/4,π/2)×(−6,∞)∪(3π/2,7π/4)×(−∞,−8)∪(3π/2,7π/4)×(−6,∞)

. : Nie. Zapisujesz [(...,...) u (...,...)] x [(....,...) u (....,....)]

klaudiusz: A×B=[(−∞,−8) u (π/4,π/2)] x [(−∞,−8) u (3π/2,7π/4)] x [(−6,∞) u (π/4,π/2)] x [(−6,∞)u(3π/2,7π/4)] B×A=[(π/4,π/2)u(−∞,−8)] x [(π/4,π/2)u(−6,∞)] x [(3π/2,7π/4)u(−∞,−8)] x [(3π/2,7π/4)u(−6,∞)]

klaudiusz: czy tak? I czym niby się różni AxB od BxA czy na rysunku to nie jest to samo?

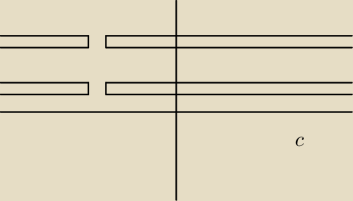
klaudiusz: czy to bedzie cos takiego dla obu przypadków?

Aruseq: Nie, to rysunek tylko do AxB

Klaudiusz: A jak zrobić BxA ? Teraz zamienia się x I y miejscami?

klaudiusz: bo nie wiem jak inaczej zeby sie roznily

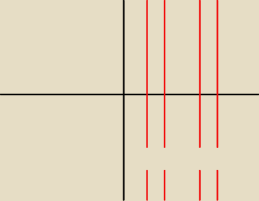
klaudiusz: cos tego typu?

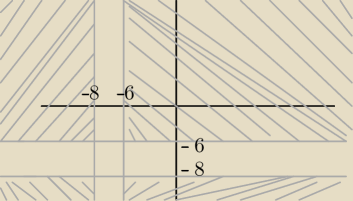
klaudiusz: i czy A x∊(−∞ ; −8) U (−6; ∞) w przypadku A² to cos tego typu?

klaudiusz: czy nie tak

. : Tak będzie A X A

klaudiusz: a czy wpis z 14:17 dobrze pokazuje BxA?

. : Na dobrą sprawe tak

klaudiusz: czyli AxB i BxA to sie zmienia jakby x i y miejscami jak sie to rysuje i stąd ta roznica?