funkcja boni qluo: wyznacz o ile istnieja f⁻¹ g⁻¹ f∘g g∘f jesli f(x) = arcsin(x−2) g(x) = √x+1 Df = [1;3] Dg= [−1; ∞] zwf = [−π/2 ; π/2] zwg = [0; ∞] czy f⁻¹ to znaczy ze funkcja jest odwrotna czy to cos innego? Czy mam szukac czy jest bijekcja?

6latek: https://matematykaszkolna.pl/forum/418432.html

boni qluo: ale nie rozumiem skad sinx = sin(arcsin(y−2) ) sinx = y−2

boni qluo: i czy f⁻¹ to inaczej funjkcja odwrotna czy to co innego

6latek: Tak f⁻¹ to tutaj symbol funkcji odwrotnej do danej funkcji Musisz pokazac ze dana funkcja jest różnowartościowa i na

boni qluo: no ale f nie jest bijekcja

boni qluo: i g tez chyba nie

6latek: Funkcja sinus(x) w swojej dziedzinie naturalnej nie jest roznowartosciowa ale w odpowiednich przedzialach jest Wiec w tym przedziale funkcja y=sinx ma funkcje odwrotna tak samo bedzie z funkcja y=arcsin(x) Funkcja g napewno jest roznowartosciowa i na Poczekaj moze wredulus sie odezwie albo chichi Oni bardziej sie w tym orientuja niz ja

wredulus_pospolitus: boni −−− dlaczego uważasz, że f(x) = arsin(x−2) nie jest bijekcją (mam nadzieję, że przeciwdziedzinę uznajesz za równą zbiorowi wartości funkcji)

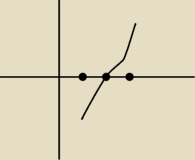
boni qluo: Rozumiem ze tutaj jest [1;3] wiec iniekcja bo wartosci Y nie sa przyjmowane wiecej niz raz a suriekcja bo kazda wartosc z przeciwdziedziny jest chociaz raz przyjmowana i nie bardzo rozumiem co tu ma sie sprawdzic czy wartosci w zbiorze wartosci od [1;3] sa przyjmowane?

boni qluo: a dobra juz wiem chyba czyli odpowiedz to jest y= sinx + 2 w przypadku odwracania f(x)?

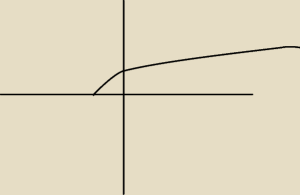
boni qluo: a czyli funkcja g(X) = √x+1 jest iniekcja bo nie przyjmuje wartosci y wiecej niz raz bo jest prosto rosnaca i suriekcja tez jest tak? Bo rozumiem że te dziedziny i zwf to ja biore prosto z funkcji tzn tutaj D= [−1; ∞] zwf = [0; ∞]

boni qluo: czyli jest bijekcja

boni qluo: x= √y+1 /² x² = y+1 y = x² + 1

boni qluo: czy nie tak

. : Sprawdź znaki

boni qluo: y = x² − 1

6latek: https://www.youtube.com/watch?v=VV94Cg0Y0cE

boni qluo: czyli teraz wynik jest ok?

boni qluo: a czy jesli chodzi o funkcje odwrotna to rozumiem ze jak mam zlozenie np g∘f to Dg ∩ Rf musi jakas istniec czyli co jak biore g∘f Dg = [−1 ; ∞] Rf = [−π/2 ; π/2] no to częsc Rf zawiera sie w Dg wiec mam rozumiec ze istnieje to zlozenie i wyglada tak g∘f = √arcsin(x−2) + 1

boni qluo: chodziło mi w 1 zdaniu o złożenie nie f odwrotna

6latek: Wobec tego ze musi się zawierac cały zbior wartosci funkcji f w dziedzinie funkcji g więc złożenie nie istnieje

boni qluo: to f∘g w takim wypadku tez nie moze byc zlozeniem tak

6latek: Według mnie tak. Obejrzyj sobie tez ten material w linku o funkcji odwrotnej