log mahatma: log₂ (cosy) < −0.5 dla y = [0; 2π] czy odpowiedz to y ∊ (π/4 ; 7π/4 )

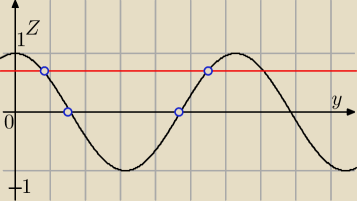
6latek: Dla mnie jest niezbyt dobrze

	1
log2(cosy)<−
	2

zakładam ze argumentem jest (y) Plus założenie co do liczby logarytmowanej cos(y)>0

	√2
log2(cosy)< log2
	2

	√2
cosy<
	2

Ja dałbym taką odpowiedz

	π		π		3		7
y∊(		,		) U (		π,		π)
	4		2		2		4

mahatma: ale to mam patrzec jak y jest mniejsze od tej liczby?

mahatma: czy na x

chichi: a gdzie ty tu masz jakieś 'x' zmienną w tej nierówności jest 'y', nie jakieś 'x'. zobacz jaką Krzysztof nadał etykietę osi poziomej

mahatma: a jesli pierwszy zbior mialem Ix+7I > 1 wyszlo mi A x∊(−∞; −8) U (−6; +∞) a w tym B wasz wynik ktory podal 6latek to jak mam sie zabrac do A X B BXA A² itp//... jak to sie robi w takich dziwnych przedzialach? Bo dobrze rozumiem ze to iloczyn karteznajnski

chichi: no i dobrze jest bo definiujemy A x B = {(x,y) ∊ R²: x ∊ A ∧ y ∊ B} czyli A jest zbiorem, którego elementy są zależne od 'x', B analogicznie − od 'y'

chichi: musisz narysować to w kartezajńskim ukladzie wspolrzednych

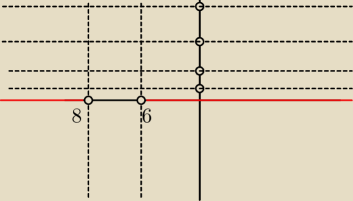
mahatma: czy cos takiego

mahatma: tam ma byc −8 i −6 a to na osi pionowej to sa te przedzialy z π