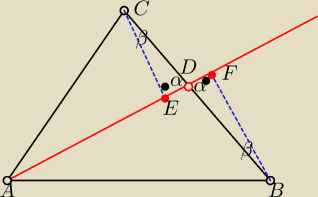
trójkąt i środkowa 6latek: W trójkącie ABC poprowadzono środkową AD . Udowodnij że punkty B i C są równo oddalone od prostej AD E i F to rzuty punktów C i B na prostą AD ΔCED ≡ Δ DFB na mocy (kbk) Sa to trójkaty prostokatne gdzie |CD|=|DB| bo punkt D to srodek odcinka BC ∡CDE=∡FDB=α jako wierzchołokowe ∡ECD=∡DBF=β=90^o−α Z przystawania tych trójkątow wynika równośc boków CE i BF Stąd wynika że punkty B i C są równo oddalone od prostej AD

wredulus_pospolitus: atlernatywnie: 1. mamy równość kątów α.

	|CE|		|FB|
2. sinα =		=		−−−> |CE| = |FB|
	|CD|		|DB|