Geom. analityczna - wyznacz równanie okręgu stycznego Monika: Dane są 3 okręgi o środkach S i promieniach r: O₁: S₁ (−3, 0) r₁=2 O₂: S₂ (0,0) r₂=1 O₃: S₃ (3,0) r₃=2 Należy wyznaczyć wzór okręgu stycznego zewnętrznie do tych 3 okręgów. Potrafię te okręgi narysować w układzie współrzędnych, zapisać ich równania i dalej nie wiem, jak dojść do równania czwartego okręgu, stycznego zewnętrznie to tych trzech okręgów. Proszę o pomoc.

Mila: Środek okręgu stycznego do trzech podanych okręgów leży na osi OY. Ułóż równanie. Pitagoras pomoże.

Monika: Mila, pojęcia nie mam, jak zapisać takie równanie

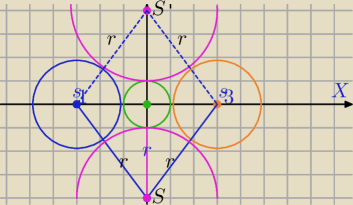
Mila: środek okręgu stycznego do trzech podanych okręgów leży na osi OY. Ułóż równanie. Teraz wiadomo?

Monika: Jaki piękny rysunek. Teraz Mila wszystko jasne. Ja miałam w wyobraźni taki okrąg, że te trzy będą wewnątrz − totalne zaćmienie. Bardzo Ci dziękuję

6latek: Dlatego ja do każdego zadania z geometrii analitycznej (choćby było najprostsze) robie rysunek .

Monika: Ja też z marszu zrobiłam rysunek tych 3 okręgów, ale czwarty okrąg w mojej wyobraźni był na zewnątrz tego "trójkąta bermudzkiego"

Mila: Sprawdź teraz, czy okrąg (x²+(y−4)²=9 ma z każdym okręgiem jeden punkt wspólny

Mila: Analogicznie dla okręgu (x²+(y+4)²=9

Monika: Dobrze Mila

Mila: ułożyłaś to równanie?