Funkcja zaba: Jak podejść do takiego zadania? Dla danej funkcji f: RxR→RxR oraz zbiorów A,B⊆RxR naszkicuj w prostokątnym układzie współrzędnych zbiór f[A]. f(x,y)=<x,x>, A={<x,y>∊RxR:x²+y²=1}

ite: f: RxR→RxR oraz f(x,y)=<x,x> Jeżeli punktowi płaszczyzny o dowolnych współrzędnych (nie ma tego jak tutaj zaznaczyć) przypiszemy punkt płaszczyzny o obu współrzędnych jednakowych i równych pierwszej współrzędnej punktu wyjściowego, to otrzymanemu zbiorowi na płaszczyźnie odpowiada prosta.

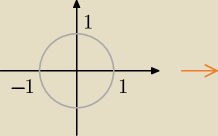
ite: W takim razie co będzie, jeżeli wybierzemy tylko punkty, których współrzędne spełniają równanie tego okręgu? Trzeba się zastanowić, jakie wartości przyjmują ich pierwsze współrzędne.

zaba: Ahh, w ten sposób to działa. Czyli będzie to prosta y=x dla −1<x<1?

zaba: Oczywiście z domkniętymi (−1) i 1

ite: Prosta jest figurą nieograniczoną, więc prosta − nie, a jej część ma swoją nazwę. Dla x=1 da się dobrać y, tak żeby równanie x²+y²=1 było spełnione.

ite: tak, przedział trzeba domknąć

zaba: Czyli na przykład gdyby zamiast warunku z okręgiem był warunek y=sin x, to byłaby to cała prosta y=x, ale już dla warunku x=sin y odpowiedź byłaby taka sama jak tutaj

ite: tak

zaba: Super, dziękuję ci ślicznie