zad matthew: Cześć, mam takie zadanie: Dwa boki trójkąta ABC mają długść 1 i 4, a jego pole jest równe 1,2. Wyznacz długość trzeciego boku tego trójkąta, jeżli wiadomo, że kąt między danymi bokami trójkąta jest rozwarty. Zrobiłem tak:

	7
P = 1,2 =
	5

	1
P =		ab * sinα
	2

	1
1,2 =		* 1 * 4 * sin(180o − α)
	2

1,2 = 2sinα

	7		1
2sinα =		/ *
	5		2

	7
sinα =
	10

7   180 o * π   10
	= 126o
π

c² = 1² + 4² − 2 * 1 * 4 * cos126^o c² = 17 − 8cos126^o c = √17 − 8cos126^o NIe jestem pewny czy dobrze je rozwiazałem.... Bardzo prosze o sprawdzenie...

matthew: Mam jeszze jedno zadanie: Długość boku kwadratu wpisanego w podstawę walca jest równa a. Wysokość walca jest równa długości promienia okręgu wpisanego w trójkąt równoboczny o boku a. Wyznacz objętość walca. Zrobiem tak...: V = 2πr(r+h)

	1
promien okregu wpisanego w trójkąt równoboczny : r =		h
	3

	1		a√3		a√3
r =		*		=
	3		2		6

promien okregu opisanego na kwadracie: d = a√2

	a√2
r =
	2

	a√2		a√2		a√3
V = 2π *		(		+		) =
	2		2		6

	a√2		6a√2 + 2a√3
= 2π *		(		) =
	2		12

	a√2		3a√2 + a√3
= 2π *		(		) =
	2		6

	6a2 + a2√6		(6a2 + a2√6)π
= 2π *		=
	12		6

tutaj również nie jestem pewny wykonania... nie mam do tych zadan odpowiedzi.. Proszę o sprawdzenie...

Godzio:

	1		a√3
H =		h =
	3		6

	1		a√2
R =		d =
	2		2

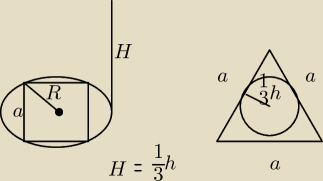
	a2*2		a√3		a3√3π
V = π R2 * H = π		*		=
	4		6		12

z tego co obliczyłem to tak chyba powinno być

matthew: ok, dzieki, a mozesz sprawdzic jeszcze pierwsze?

Godzio: po pierwsze

	6
1,2 =
	5

matthew: masz racje, pomylka ....

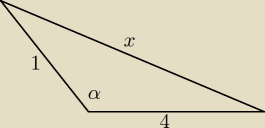
Godzio: 90<α<180

1
	* 4 * sinα = 1,2
2

sinα = 0,6 sin²α + cos²α = 1

	64
cos2α =
	100

cosα = 0,8 x² = 1² + 4² − 2*4cosα x² = 17 + 8 * 0,8 x²= 23,4

	3√55
x =
	5

a tak tego by nie można było zrobić? tylko nie wiem po co ta informacja o tym kącie

matthew: wiesz co.... w drugim zadaniu skorzystałem nie z tego wzoru co trzeba.... ech... liczyłem pole a nie objetośc... a w pierwszym spróbuje zrobic tym samym sposobem tylko oczywiscie poprawie blad i zapisze go tutaj.... Dzieki za odpowiedzi

matthew: .... to nie potrzebnie przekształcałem kąt podany w mierze łukowej?....

matthew: a juz chyba wiem dlaczego.... we wzorze na twierdzenie cosinusow wystepuje cosinus, a nie sinus..... ok rozumiem

Godzio:

matthew: mam jeszcze takie zadanie: Wyznacz wierzchołki trapezu równoramiennego ABCD, |AB| > |CD| i AB || CD, mając równanie jego

	1
osi symetrii y = −		x + 2 i wiedząc, że jej punkty przeciecia z osiami układu
	2

współrzędnych są środkami podstaw, punkt A = (1, −6), a jedna podstawa jest dwa razy większa od drugiej. Zacząłem tak: A = (1, −6) liczę prostą prostopadłą do prostej y.....

	1
−		a = − 1
	2

a = 2 y = 2x + b −6 = 2x + b b = −8 y = 2x − 8 obliczam punkt P, który jest średnią długości odcinka |AB|

	1
{y = −		x + 2
	2

{y = 2x − 8 x = 4 y = 0 P(4,0) znajduje punkt B:

	1+x		−6 + y
4 =		/ *2 0 =		/ *2
	2		2

8 = 1 + x 0 = −6 + y x = 7 y = 6 B(7,6) |AB| = √(1 − 7)² + (−6 −6)² = 6√5

|CD|		1
	=
|AB|		2

2|CD| = |AB| 2|CD| = 6√5 |CD| = 3√5.... mam długośc odcinka |CD| ale nie wiem jak obliczyć wpółrzędne tych pkt..... nie jestem pewny czy dobrze zrobiłem pierwsza czesc zadania... Proszę o pomoc....

Godzio: już pomagam, pozwolisz ze zrobie na swoj sposob a ty sprawdzisz poprawnosc rozwiazan

matthew: oczywiscie w miare mozliwosci pozwole sobie na ten zaszczyt

Godzio: już skończyłem tylko zrobie sobie rysunek rzeczywisty zeby sprawdzic czy wszystk ok

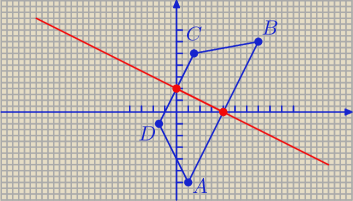
Godzio: Najpierw B: wyliczając punkty przecięcia prostej z osiami wspolrzednych otrzymujemy: S(0,2) => środek DC O(4,0) => środek AB mając dane A liczmy B

	1+xb		−6+yb
O = [4,0] = [		,		]
	2		2

	1+xb		−6+yb
4 =		0 =
	2		2

8 = 1 + x_b 0 = −6+y_b x_b = 7 y_b = 6 B(7,6) czyli to Ci wyszło ok długość AB: AB = √(1−7)² + (−6−6)² = √36+144 = 6√5 CD = 3√5 D i C :

	1
prosta prostopadła do prostej y = −		x + 2 i przechodząca przez środek DC :
	2

a = 2 , S(0,2) 2 = 2*0 + b b = 2 y = 2x + 2 długość SC: |SC| = √x² + (y−2)² = 1,5√5 /² i podstawiamy naszą prostą x² + 4x² = 11,25 5x² = 11,25 x² = 2,25 Cx = 1,5 v D x = −1,5 y = 5 v y = −1 wszystko ok sorki że tak długo ale rysunek nie chciał mi poprawnie wyjść bo inne skale przyjąłem

matthew: ok wszystko juz rozumiem... no tzn. prawie dlaczego akurat należało stworzyć układ równań z prostą oraz długością ZC? Zdaję sobie sprawe, ze gdyby nie takie podejscie to pewnie nie mielibyśmy rozwiązania, ale dziwne dla mnie to troche jest. np. jezeli chce zanalezc punkt przeciecia dwóch prosty to należy ich wzory podstawic do układu. Ok. wiem to, ponieważ taka jest jedna z wielu własności... i wiem tez w jakich przypadkach sie z niej korzysta, zeby np,. ulatwic sobie liczenie, czy tez skrócić. Chodzi mi po prostu o to, czy ten sposob, ktorego uzyłeś, stosuje sie w jakichś konkretnych przypadkach? Szczerze mowiąc pierwszy raz spotykam się z takim rozwiazaniem, tzn. zeby z układu, w którym znajduje sie wzór prostej prostopadłej oraz długość jakiegoś odcinka, która jest częścią wspólną tej prostej obliczyć współrzędne... i jeszcze to: |SC| = √x² + (y−2)² = 1,5√5 / ² czy to jest poprawny zapis? ... fachowy? przepraszam, ze sie czepiam jest to dla mnie istotne, ponieważ moj nauczyciel jest dosyć drobiazgowy.... dziekuje za odpowiedz

Godzio: naczy ja to robie na oko to co mi podpasuje to robie ,ale prostą prostopadłą która przechodzi przez C i D to raczej trzeba obliczyc bo bez niej to ciezko bedzie znalesc te punkt, a ten zapis to chyba dobry przynajmniej ja nic zlego w nim nie widze