Asymptota
Maniek12: Znajdź asymptoty
f(x)= (3x)/(3x−2x)
14 lis 19:45
wredulus_pospolitus:
1. dziedzina
2. sprawdzamy asymptotę pionową
3. sprawdzamy granice w ±
∞
W czym problem

14 lis 22:49
b:
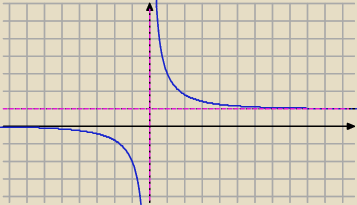
14 lis 22:56
Maniek12: A co bedzie dziedziną?
15 lis 09:35
Zenek z fabryki syrenek: masz wykres i dziedziny nie potrafisz odczytać?
15 lis 09:38
Maniek12: To ze jest bez 0 to widze ale z jakiego rownania ono wynika
15 lis 10:33
Maniek12: Czyli wychodzą przedziały (−∞;0) u (0;+∞)
Czyli
lim (30)/(30−20)
x→0−
i
lim (30)/(30−20)
x→0+
Wydaje mi sie ze dobrze tylko nie wiem jak rozwiazac te granice
15 lis 10:53
Fałszywy 6-latek: w matfizie jesteś to powinni ci podać metody do takich granic, wyciągasz cos przed nawias z
licznika i z mianownika
15 lis 11:31
Jolanta: 30=1 20=1. 1−1=0 w mianowniku nie może być 0 czyli x≠0
15 lis 12:20
Litlle Mint:
| | 3x | | 3x/3x | | 1 | |
f(x)= |
| = |
| = |
| stad x≠0 bo |
| | 3x−2x | | | | | |
(2}{3}
0=1 i mianownik sie bedzie zerował
15 lis 13:00
Maniek12: Okej rozumiem a jak rozwiazac te granice?
15 lis 13:02
jc: Nie trzeba przekształcać, aby zobaczyć, że dla x=0 mamy dzielenie przez zero.
Dla x>0 mianownik jest dodatni, a dla x<0 ujemny.
15 lis 13:03

