Równanie W: Rozwiąż równanie

	πx
x2−4x−sin		+5=0
	4

ite: W takich sytuacjach trzeba wierzyć, że dane zostały dobrane w życzliwy sposób i sprawdzić, czy równanie

	πx
x2−4x+5=sin
	4

będzie mieć rozwiązania. Czyli ustalić, jaki jest zbiór wartości wyrażenia z lewej strony równania.

W: Dzień dobry x²−4x+5=0 (x−2)²+1=0 q=1 Z_w=<1,∞)

	πx
sin		=1 i x2−4x+5=1 dla x=2 bo muszą być rowne
	4

	πx
sin		=1
	4

πx		π
	=		+2kπ i k∊C i x=2
4		2

x=2+8k k∊C i x=2

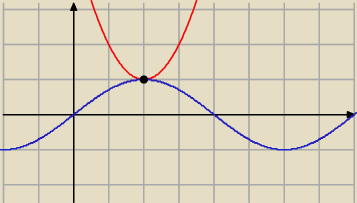Saizou : Tak jak pisze ite. f(x)=x²−4x+5 = (x−2)²+1 →ZW = [1; +∞]

	π
g(x) = sin		x →ZW = [−1,1]
	4

zatem jedynym elementem wspólnym jest 1. Stąd mamy do rozwiązania równanie

	π
1 = sin		x
	4

π		π
	x =		+2πk, gdzie k∊Z
4		2

x = 2+8k

W: Dzięki Saizou