 Dane są zbiory
A={x∊R: x5−4x3−8x2+32≥0
B={x∊R: log0,1(4−x2>log0,1(6x−3)
a) Wyznacz zbiór AUB oraz A∩B
b*) Wyznacz zbiór (A\B)∩C gdzie
C={x∊R: (√2+√3)x+(p[2−√3})x<4
Zbiór A)
x5−4x3−8x2+32≥0
x3(x2−4)−8(x2−4)≥0
(x3−8)(x2−4)≥0
x3−8=(x−2)(x2+2x+4)=0 to x=2
x2−4=0 to x=2 lub x=−2
x=2 pierwiastek podwójny i x=−2 pojedynczy
x5−4x3−8x2+32≥0
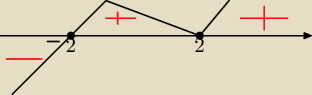
dla x∊[−2,∞)
Zbiór B )
Założenia
4−x2>0 to x∊(−2,2)
6x−3>0 to x>2
D=(−2,2)
log0,1(4−x2)>log0,1(6x−3)
4−x2<6x−3
−x2−6x+7<0
x2+6x−7>0
Δ=36+28=64
Dane są zbiory
A={x∊R: x5−4x3−8x2+32≥0
B={x∊R: log0,1(4−x2>log0,1(6x−3)
a) Wyznacz zbiór AUB oraz A∩B
b*) Wyznacz zbiór (A\B)∩C gdzie
C={x∊R: (√2+√3)x+(p[2−√3})x<4
Zbiór A)
x5−4x3−8x2+32≥0
x3(x2−4)−8(x2−4)≥0
(x3−8)(x2−4)≥0
x3−8=(x−2)(x2+2x+4)=0 to x=2
x2−4=0 to x=2 lub x=−2
x=2 pierwiastek podwójny i x=−2 pojedynczy
x5−4x3−8x2+32≥0
dla x∊[−2,∞)
Zbiór B )
Założenia
4−x2>0 to x∊(−2,2)
6x−3>0 to x>2
D=(−2,2)
log0,1(4−x2)>log0,1(6x−3)
4−x2<6x−3
−x2−6x+7<0
x2+6x−7>0
Δ=36+28=64
| −6−8 | ||
x1= | =nie należy do dziedziny | |
| 2 |
| −6+8 | ||
x2= | =1 −nalezy do dziedziny | |
| 2 |
| (√2+√3*√2−√3 | 4−3 | 1 | ||||
√2+√3= | = | = | ||||
| √2−√3 | √2−√3 | √2−√3 |
| 1 | ||
t+ | <4 | |
| t |
| 1 | ||
t+ | −4<0 | |
| t |
| 4−2√3 | ||
t1= | =2−√3>0 | |
| 2 |

