Nierówność i parametr W: x²−3x+2<0 Δ=9−8=1

	3−1
x1=		=1
	2

	3+1
x2=		=2
	2

x∊(1,2) Pytanie: Dla jakiej wartości parametru a zbiór rozwiązan tej nierówności jest zawarty w zbiorze rozwiązań nierówności ax²−(3a+1)x+3>0 We wskazówce do zadania jest napisane aby rozpatrzyc 5 przypadków w zależności od kształtu i polożenia drugiej nierówności

	1		1		1
1)a=0 ,2)a=		3) a∊(0,		) 4) a∊(		,∞) 5) a<0
	3		3		3

Wytłumaczy ktoś dlaczego tak?

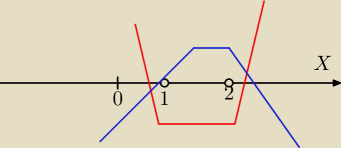
Maciess: Zacznij od narysowania tej sytuacji

wredulus_pospolitus: 1. aby to miało ręce i nogi ... to a<0 (bo tylko wtedy będziemy mieli przedział ograniczony z góry i z dołu) 2. wtedy jeszcze musi być prawdą: f(x) = ax² − (3a+1)x + 3 , f(1) < 0 ∧ f(2) < 0 , x_wierzchołka ∊ (1;2)

W: Policzyłem deltę z równania drugiego Δ=[−(3a+1)]²−12a Δ=9a²+6a+1−12a= 9a²−6a+1= (3a−1)² √Δ=|3a−1|

	1
dla a<		|3a−1|=1−3a
	3

	1
dla a≥		|3a−1|=3a−1
	3

Nie wiem czy ide w dobrym kierunku w ogóle

Jolanta: w dobrym Nierównosc spełniona jest dla x∊ (1.2) 1. Dla a=0 nirównośc ma postac −x+3>0 zbior rozwiązan zawiera przedział(1,2) 2.a≠0 i to co robisz

www: https://zadania.info/d568/7379946

W: Dziękuje . D;la a=0 bedziemy mieli nierownośc liniową Potem zrobię też to co zaproponował wredulus_pospolitus

W: Podziękowania równiez dla www za poświęcony czas .