proszę o rozwiązanie anna: Kamil chce ustawić 13 książek na dwóch półkach Na wyższej półce ma stać w szeregu 7 książek a na niższej mają stać w szeregu pozostałe książki na ile sposobów można ustawić wszystkie książki tak aby książki A B C stały obok siebie

Monika: Zanim jakaś mocna głowa to zad. rozwiąże, podpowiem Ci, że te 3 książki ABC potraktuj jako jedną, po prostu zwiąż je sznurem, żeby zawsze były razem. Oczywiście w tej trójce książki będą się mieszać, bo mogą być ustawione: ABC, ACB, BCA, BAC, CBA, CAB, więc tej trójce dasz 3 silnia. I tyle wiem. Gdyby miały stać w szeregu to 10 silnia * 3 silnia, ale skoro są one ustawiane na 2 półkach, to nie wiem, jak dalej, ale chętnie się dowiem.

wredulus_pospolitus: jako, że mamy dwie półki i podane ile książek ma być na danej półce to mamy musimy przyjąć dwie opcje:

	10 4
1. ABC jest na górnej półce −−− wtedy mamy		*3!*5!*6!

czyli kolejno: wybieramy 4 książki, które razem z ABC będą na górnej półce permutujemy ABC. permutujemy te 4 książki i 'zestaw' ABC na górnej półce permutujemy pozostałe 6 książek na dolnej półce 2. ABC jest na dolnej półce −−− spróbuj to zrobić samodzielnie −−− będzie analogicznie do tego co powyżej napisałem

anna: nadmieniam że wynik to 54*10!

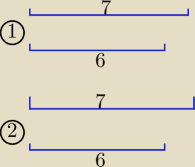
a: 1/ jak podał wredulus

	10 4		10!
		*3!5*4!*6! =		*3!*5*4!*6!= 10!*5*6=30*10!
			4!*6!

	10 3		10!
2/		*3!*4*3!*7! =		*3!*4*3!*7!} =10!*24
			3!*7!

Razem : 30*10!+24*10!= 54*10!

anna: dziękuję bardzo