parametr m, wartosc bezwzgledna podjeyfa: |mx|+|m|=4 Dla jakich wartości parametru m podane równanie ma dwa rozwiązania? proszę o pomoc

Maciess: https://www.geogebra.org/calculator/uwfgqeee Na start pobaw się tym i coś zaobserwuj

Maciess: Pytania pomocnicze. Czy wykres funkcji |mx|+|m| jest symetryczny względem osi Y? (Jesli tak do odpowiedz sobie dlaczego) Jak to wpływa na rozwiązania tego równania? Czy funkcja |mx|+|m| może przyjąć wartości ujemne? A tak w ogóle to pytaj i będziemy pomagac

wredulus_pospolitus: |mx| + |m| = 4 |m| * |x| + |m| = 4

	4
|x| + 1 =
	|m|

	4
|x| =		− 1
	m|

	4		4
tak więc... równanie będzie miało dwa rozwiązania (		− 1 oraz −		m}} + 1)
	|m|

	4		4
jeżeli		− 1 > 0 −−−>		> 1 −−−> |m| < 4 −−−> m ∊ jakiego przedziału
	|m|		|m|

wredulus_pospolitus: po drodze zapomniałem o pewnym (ale jakże oczywistym) założeniu

Maciess: no i popsuł zabawe Sprawdzić m=0 na starcie i masz komplet.

podjeyfa: czyli odpowiedź to będzie m∊(−∞,−4)u(−4,4)u(4,+∞)

6latek : No nie m∊(−4,4) jest m=0 a mozna dzielic przez 0?

podjeyfa: zapomniałem dopisać ale m≠0 i nie do końca rozumiem czyli jaka będzie odpowiedź

wredulus_pospolitus: m ∊ (−4;4) \ {0}

podjeyfa: no właśnie tak wychodzi z pierwszego rozwiązania, a co z drugim? bo w nim mi wyszło właśnie m∊(−∞,−4)u(4,+∞), co mogło pójść nie tak

6latek : |m|<4 to m<4 i m>−4

podjeyfa: no to wiem, tak mi wyszło z pierwszego rozwiązania, ale coś zepsułem z drugim i nie wiem czemu

6latek : Nie wiem jakie masz rozwiazania wiec je napisz tutaj ktos zawsze odpowie .

podjeyfa: przecież są wyżej

chichi: tak naprawdę nie trzeba nawet wykonywać dzielenia które wykonał wredulus. następuje parametryzacja zmiennej, więc zerkamy pierw co się stanie, gdy się wyzeruje. jak już sprawdzimy zakładamy, że m ≠ 0, wówczas równanie zapisujemy w postaci: |mx| = 4 − |m|, zatem 2 rozw. iff 4 − |m| > 0 ⇔ m ∊ (−4,4) na koniec wyrzucamy z tego przedziału bądź też nie, te wartość która zerowała uzmienniony wyraz, to należało sobie odpowiednio wcześniej sprawdzić. podać odp. końcowa i voilà

podjeyfa: równanie będzie miało dwa rozwiązania (4/|m| −1) oraz (−4/|m| +1) no i z tego pierwszego faktycznie wychodzi m∊(−4,4)\{0} ale ale co z drugim

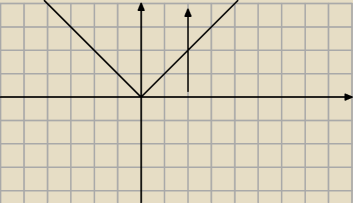
6latek : masz wykres funkcji y=|x|

	4		4
Więc to rownanie |x|=		−1 bedzie miało dwa rozwiazania x=		−1 oraz
	|m|		|m|

	−4
x=		+1
	|m|

wtedy gdy

	4
Prawa strona tego rownania |x|=		−1 bedzie leżec nad osia OX czyli musi być
	|m|

	4
		}−1>0
	|m

WIdzisz ze <0 nie moze byc bo wtedy nie ma rozwiazan Musimy rozwiazac ta nierownosc

4
	−1>0 i m≠0
|m|

Wartosc |m| jest zawsze dodatnia wiec nie zmieni sie zwrot nierownosci 4−|m|>0 −|m|>−4 |m|<4 a to juz jest nierownosc elemntarna m<4 i m>−4 zaznaczasz na osi i masz przedzial m∊(−4,4)\{0} Wez sobie pare wartosci m z tego przedzialu i sprawdz Takze wez sobie 2 −3 wartosci z poza przedziału i zobacz co sie dzieje dla m=−5 |−5|=5

4
	−1 jakie to wyrazenie jest ? dodatnie czy ujemne ?
5

pamietaj ze maja być >0