wyznacz paprotka: Wykaż, że równanie x⁴−x²−2x+4=0 nie ma pierwiastków rzeczywistych.

jc: oblicz (x²−1)² + (x−1)²+2

chichi: mniej ambitny sposób, to pokazać, że minimum wielomianu to 2 dla x = 1, to widać też z wielomianu, który napisał @jc ale badając pochodną otrzymasz ten sam wniosek

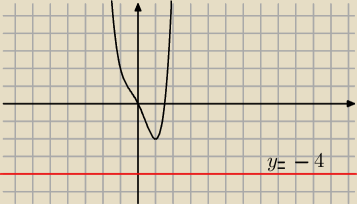
q: y=x⁴−x²−2x (czarny wykres ) kilka punktów i masz wyobrażenie jak wygląda y=−4 czerwony wykres nie przecina w żadnym punkcie czarnego wykresu

chichi: to nie jest dowód.

q: Niechaj i tak będzie jak piszesz (nie dochodzę sie) Jesteśmy obecnie na wielomianach po funkcji kwadratowej Wyznaczc minimum i maksimum funkcji kwadratowej (czy to na podanym przedziale czy nie ) umiemy Tutaj mamy wielomian stopnia czwartego . Nie znamy jeszcze całego aparatu do badania takich funkcji ,ale wiemy tylko jak szukac pierwiastkow całkowitych czy wymiernych . Jak postąpisz wtedy? To może byc juz student ale nie jest powiedziane ze tak jest

chichi: znamy aparaturę znajdowania ekstremow dowolnych funkcyj, zwłaszcza wielomianowych

q: No właśnie nie znamy

chichi: a jak zamkniesz oczy, to cie nie widać. daj se siana gościu...

q: Zobacz co napisałem o 14:02 −nie znamy ....

q: Jeśli zapytasz przedzszkolaka ile to jest 2+2, to odpowie pewnie 4 A potrafisz to udowodnić? No nie . Jak to nie potrafisz? Nie znasz aparatury zeby to udowodnic? Właśnie w ten sposób potraktowałes mnie

chichi: ty mówisz nie znamy − jakoby w matematyce nie była znana takowa. jeśli ty jej nie znasz, to nie znaczy, ze ona nie istnieje. piszesz bzdury, więc należycie ci odpowiedziałem.

ABC: on chciał to zadanie zrobić na poziomie 2 klasy LO profilu podstawowego − jest to dosyć ambitne wyzwanie

q: chichi Napisałes że to nie jest dowód . Zrobiłem to ma miare swoich wiadomosci . Tzn wiem jak wykonac wykres (bo można rozwiązac równanie graficznie ) Tak powiedziała w szkole Pani. Moglem też ewentualnie pokazać ze nie istnieja pierwiastki wymierne Jestem przed granicami i pochodnymi . Czy na chwile obecna musi byc juz mi znana ta aparatura? Więc jak należycie odpowiedziałes (daj se siana ?

chichi: jak byś wykonał ten wykres? skąd wiedziałbyś, że monotoniczność zmienia się w 1? bez aparatury badania przebiegu zmienności funkcji to ty sobie możesz jedynie rysować przybliżone szkice. no chyba, że wklepiesz sobie w program

chichi: a ty z granicami miałeś zapewne do czynienie gdy mnie jeszcze dawno w planach nie było, tylko ciągle się cofasz i robisz wszystko od początku. nie wiem do czego zmierzasz...

chichi: nawet pamiętam jak uczyłeś kogoś na tym forum uczyć pochodne funkcji złożonych, o czym ty mówisz to ja nie wiem...

q: Dobrze Są ku temu bardzo poważne powody

q: chichi To wszystko nieważne ale chciałem to zrobić tak jak pisze ABC

ABC: Małolat , nie wiem kto uczy twoje wnuki , ale panie w szkole mają teraz duże braki

q: ABC Moje wnuki uczy ten co go Wanda nie chciała

ABC: to u nich też jest kiepsko , bo polskich nauczycieli chcą zatrudniać

Wanda: Jak się połaczymy to i Ty się załapiesz

ABC: miałem taki przypadek parę lat temu , u nas w Polsce nie chcieli mnie wpuścić do jednej instytucji, dobijamy się i nikt nie otwiera drzwi. Wtedy miałem błysk , przypomniałem sobie okupację i jak nie ryknę :Aufmachen! , kilka sekund i drzwi się otworzyły

6latek : Wróćmy jednak do tego równania . Okazaliśmy ze nie posiada ono pierwiastków wymiernych Teraz na to żeby to równanie nie posiadało rozwiązań rzeczywistych nie może mieć rozwiążań niewymiernych Jak to pokazac ? Czy może potrzebny jakiś dowód?

k: Zostało już pokazane o 8:53.

ABC: https://zadania.info/d251/2088835 tu masz małolat ciekawą dyskusję podobnego zadania

6latek : Witam Dziękuje . Zaraz zobaczę. Probowałem wczoraj rozwiazac to rownanie ale przy wyodrebnianiu pelnych kwadratów wyszlo nieciekawie wiec zostawiłem A dzisiaj nie z roboty?

Fałszywy 6-latek: teraz dopiero z roboty , bezpośrednie rozwiązanie tego równania to kaliber Mariusza , ja bym odpuścił na twoim miejscu

6latek : Doszdełem do λ³+λ²−16λ−20=0 i tu sobie zostawiłem bo myslalem ze wyjdzie jakis ladny rzeczywisty pierwiastek

Fałszywy 6-latek: niestety nie wychodzi