Injekcja Butek: Funkcja f : X → Y jest injekcją wtedy i tylko wtedy, gdy zachodzi następujący warunek: ∀ x 1 , x 2 ∈ X : f ( x 1 ) = f ( x 2 ) ⟹ x 1 = x 2 . Mógłby ktoś to wytłumaczyć? Czemu taki zapis że x₁ = x₂ co to ma do injekcji

. : Iniekcja czyli różnowartościowość funkcji. Powyzszy zapis oznacza że jeżeli funkcja przyjmuje taka sama wartość dla x₁ i x₂ to oznacza że muszą one być sobie równe (bo tylko wtedy funkcja nie przestaje być funkcja różnowartościowościowa.

. : Inna wersja może być zapis: ∀_x1 ∀_x2 x₁ ≠ x₂ ⇒ f(x₁) ≠ f(x₂)

Butek: Ale nie rozumiem co ma injekcja do dwóch takich samych funkcji Jak mam f(x) = 2x +1 I chcę sprawdzić Czy jest Injekcja Surjekcja Bijekcją Jak to można zrobić?

wredulus_pospolitus: niee ... to nie są 'dwie takie same funkcje' tu chodzi o dwa argumenty funkcji. A co do Twojego pytania −−− nie wiemy jaka jest dziedzina i przeciwdziedzina ... więc nie mogę odpowiedzieć na to pytanie. Jesteś na studiach −−− więc warto by było przynajmniej dokładnie przepisywać zadanie.

wredulus_pospolitus: dla funkcji f(x) = 2x + 1 To co Ty podałeś by oznaczało, że: Jeżeli 2x₁ + 1 = 2x₂ + 1 to oznacza, że x₁ = x₂. Co oczywiście jest prawdą, bo wykresem funkcji f(x) = 2x+1 jest prosta rosnąca, więc funkcja oczywiście, że będzie funkcją monotoniczną (przez co także różnowartościową).

wredulus_pospolitus: natomiast gdybyśmy wzięli sobie funkcję g: R−>R g(x) = x² to już zapis: Jeżeli x₁² = x₂² to oznacza, że x₁ = x₂ by nie był prawdą ... bo przecież dla na przykład: x₁ = −1 i x₂ = 1 prawdą będzie, że x₁² = (−1)² = 1 = 1² = x₂² a przecież x₁ ≠ x₂

Butek: No ja rozumiem te kryteria Ale jak dwa punkty w takiej zwykłej funkcji mogą się równać Nie rozumiem w funkcji 2x+1 nie ma dwóch takich samych x tym bardziej z tymi samymi y

wredulus_pospolitus: No to właśnie nie rozumiesz tego 'kryterium'.

6latek: To napisz jak badamy funkcje czy jest ona róznowartosciowa

6latek: Weżmy ta co napisałes f(x)=2x+1

wredulus_pospolitus: Może w ten sposób −−− mamy funkcję f(x) = 2x + 1. Funkcja ta będzie różnowartościowa jeżeli prawdą będzie to stwierdzenie: Jacek wybiera sobie jakiś dowolny (ale w dziedzinie) 'x' i sprawdza wartość funkcji dla tego 'x' którego wybrał. Marek także wybiera sobie jakiś dowolny (ale w dziedzinie) 'x' i sprawdza wartość funkcji dla swojego 'x'. Jeżeli wartość funkcji dla Jackowego 'x' jest równa wartości funkcji dla Markowego 'x' ... to oznacza, że obaj wybrali dokładnie taki sam 'x'. I jeżeli jest to prawda dla każdego możliwego 'x' jakiego mógłby wybrać Jacek oraz dla każdego możliwego 'x' jakiego mógłby wybrać Marek −−−− wtedy funkcja f(x) jest różnowartościowa.

Butek: No to dość oczywiste Ale jak to sprawdzić algebraicznie mając wzór funkcji

wredulus_pospolitus: udowodniając to

wredulus_pospolitus: 2x₁ + 1 = 2x₂+1 ⇔ 2x₁ = 2x₂ ⇔ x₁ = x₂ i gotowe

wredulus_pospolitus: ale tak jak na początku napisałem −−− nie podałeś dziedziny i przeciwdziedziny tejże funkcji

Butek: Ale to trzeba na jakiś konkretnych liczbach wpisać że dla x jest tylko jeden y czy jak

wredulus_pospolitus: Nie ... nie masz nic robić na konkretnych liczbach. Dowodów prawdziwości, że coś zachodzi 'dla ogółu' nie przeprowadza się dla konkretnej liczby ... chyba że przeprowadzisz to dla KAŻDEJ z możliwych liczb (życzę powodzenia). Dowodzenie nieprawdziwości, że coś zachodzi 'dla ogółu' można dokonać poprzez podanie konkretnej liczby (przypadku) dla którego to nie zachodzi −−− bo wystarczy jeden taki przypadek i zdanie "to jest prawdą dla dowolnego x" upada.

6latek: Kłóć się troche z wredulusem Dla tej konkretnej funkcji f(x)=2x+1 jeśli nie podano dziedziny to przyjmuje sie ze dziedzina takiej funkcji będzie jej naturalna dziedzina Tutaj zbiór liczb rzeczywistych

6latek: Takie pytanie Naprawdę nie masz żadnego przykładu rozwiązanego w podręczniku? Nie chce mi sie wierzyć

ABC z roboty: "Butek: Ale to trzeba na jakiś konkretnych liczbach wpisać że dla x jest tylko jeden y czy jak" jeżeli on jest na takim poziomie zrozumienia , to zacząć trzeba byłoby od tego jaki kwantyfikator występuje w definicji funkcji różnowartościowej ,jak się dowodzi zdania zawierającego taki kwantyfikator, jak się zaprzecza takiemu zdaniu. Ale to jest orka na ugorze ja się nie podejmuję

Butek: Wyznacz o ile istnieją f⁻¹ g⁻¹ f•g g•f Jeśli F(x) log₂ (x+1) G(x) = x² −1

. : Dziedzina przeciwdziedzina funkcji f i g?

Butek: Nie ma nic podane

6latek: Ale to powinienes wiedzieć sam Po drugie jaka postac na funkcja f i g bo F i G to widzę

wredulus_pospolitus: f(x) = log₂(x+1) g(x) = x²−1 1. Proszę podać dziedziny i zbiory wartości tych funkcji 2. Proszę pokazać czy są różnowartościowe 3. Sprawdzanie czy są 'na' nie ma sensu jeżeli przyjmiemy ZW jako przeciwdziedzinę 4. W przypadku złożeń − sprawdzić czy ZW jeden funkcji zawiera się w dziedzinie drugiej (wtedy odpowiednie złożenie jest możliwe)

6latek: Witaj Wiem jestem juz stary i przez to bardzo upierdliwy Ale dlaczego zmieniłes zapis funkcji ?

wredulus_pospolitus: 6latek −−− bo nie chce mi się przepychać w wołem

6latek: Dobrze

6latek: Zeby ją /jego zachęcic do działania wiec funkcja f(x)= log₂(x+1) jest funkcja logarytmiczna co widzac i czuc Masz log_a b =c ⇔a^c=b jakie warunki musi spelniac ten logarytm log_ab żeby był okreslomy ?

Butek: https://ibb.co/PGK0Qq1 Co dalej muszę zrobić? One mają być roznowartosciowe czy bijekcją? I z czego wynika ten warunek ? I co macie na myśli że ZW zawiera się w dziedzinie drugiej funkcji. I jak wyznaczyc tą funkcję? Ja mam to narysować? Bo wiem tylko że pod x podstawia sir y

wredulus_pospolitus: 1. "Co dalej muszę zrobić? " −−− pytasz się odnośnie czego? Fotki którą załączyłeś? A skąd mamy wiedzieć ... polecenia nie znamy I niby skąd ta pewność że obie funkcje są bijekcjami? Jakoś szkice wykresów średnio mnie przekonały. 2. "One mają być roznowartosciowe czy bijekcją?" a skąd mamy to wiedzieć skoro treści zadania nie mamy ?! 3. "I z czego wynika ten warunek ?" heeee Jaki warunek 4. "I co macie na myśli że ZW zawiera się w dziedzinie drugiej funkcji." żeby złożenie miało sens − ZW funkcji 'wewnętrznej' musi się zawierać w dziedzinie funkcji zewnętrznej. Przykład gdy tak nie jest: f: R −> (−∞, −1] : f(x) = −x² − 1 f: [0 ; +∞) −> [0 ; +∞): g(x) = √x z oczywistych względów funkcja g(f(x)) = √ (−x² − 1) nie ma sensu

wredulus_pospolitus: Swoją drogą −−− czy złożenia funkcji i funkcja odwrotna to nie jest część materiału szkoły średniej

butek: wiadomosc o 10:27

butek: ma polecenie

butek: no ale jak dziedziny maja sie pokrywac to czemu mowa o ZW jak rozumiem zbiorze wartosci

wredulus_pospolitus: a gdzie ja mówię o tym że dziedziny mają się pokrywać

6latek: Pytanie Kiedy mówimy ze jakas funkcja h(x) ma funkcje odwrotną ? Patrzy na definicje i pisze

Butek: No ale czemu dziedzina ma się pokrywać że zwf?

6latek: Zadałem Ci konkretne pytanie ,dlaczego na nie nie odpisujesz ?

chichi: jak można pisać np. funkcja f(x), h(x) często na tym forum spotykam takie stwierdzenie, każdy to olewa, a to nie jest żadna funkcja...

Butek: funkcja jest odwracalna wtedy, i tylko wtedy, gdy dla każdego argumentu istnieje odpowiadająca mu jedna wartość.

6latek: Pytałem kiedy posiada funkcje odwrotną? teraz zeby nie mylic z twoimi oznaczeniami Mamy funkcje h:Y→X oraz funkcje k:X→Y Moje pytanie jest takie Kiedy funkcja h bedzie funkcja odwrotną do funkcji k

6latek: Jeszcze dopiszę X=D(k) , Y=ZW(k)

butek: no na tym polega moje pytanie

6latek: Nie kolego . Nie na tym polega . Wybacz ale nie na tym polega . Ty masz spojrzeć do definicji a w definicji jest wyrażnie napisane kiedy

Butek: Nie rozumiem co usilujesz zrobić Zadałeś pytanie kiedy funkcja ma f odwrotna

Butek: W ogólności, funkcja jest odwracalna wtedy, i tylko wtedy, gdy dla każdego argumentu istnieje odpowiadająca mu jedna wartość

6latek: https://zapodaj.net/plik-G1ighmCYKg

6latek: Moje pytanie dotyczyło tej pierwszej definicji

butek: co oznacza R (f) = Y czy mozemy ostatecznie dojsc do tej odpowiedzi jak to zrobic

q: Jest to starsze wydanie wiec R oznacza zbior wartosci R=ZW Na samym dole masz wyjasnienie co oznacza .Wlasnie to przyda sie kiedy kiedy bedziesz dokonywał zlozenia funkcji czyli np fog Wezmy teraz ta g(x)= x²−1 czy ta funkcja ma funkcje odwrotna?

Butek: No właśnie o to pytam Jak sprawdzić czy ma Ta definicja nic mi nie mówi

Butek: a niedługo minie doba od rozwiązywania tego problemu

q: Masz skan i patrz co pisze . Zreszta sam o tym pisałes jaka wyjsciowa funkcja musi być (rózmowartosciowa i na ) Ze mna masz od 19 cos i ja tez nie jestem w stanie z Toba cały czas siedziedz bo mam tez rodzine

jc: f : X →Y funkcja odwrotna istniej ⇔ dla każdego y ∊ Y równanie f(x)=y ma dokładnie jedno rozwiązanie x∊ X. Piszemy wtedy x=f⁻¹(x). Co się może zepsuć? dla pewnego y równanie może nie mieć rozwiązania (funkcja f nie jest suriekcją); dla pewnego y równanie ma więcej niż jedno rozwiązanie (funkcja nie jest różnowartościowa). Przykład 20:49 X=R, Y=R, f(x)=x²−1. Równanie f(x)=−2 nie ma rozwiązania (już to wystarczy aby nie dało się funkcji odwrócić). Równanie f(x)= 0 ma dwa rozwiązania. Ograniczając X i Y można sprawić, że funkcja określona tym samym wzorem będzie odwracalna. Tu np. można przyjąć: X=[0,∞), Y=[−1,∞) lub X=[1,∞), Y=[0,∞) lub jeszcze inaczej.

q: WItaj jc On juz z liceum czy technikum powinien wiedziedz ze funkcja y=x² nie jest różnowartosciowa na całej dziedzinie i takze umiec to wykazać

Butek: no tylko chyba nie o tych funkcjach jest mowa w poleceniu

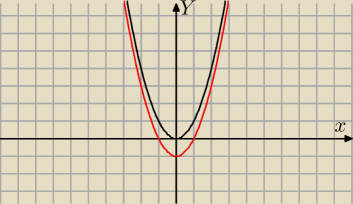
q: Funkcja y=x²−1 (czerwony wykres ) rózni sie tylko tym od funkcji y=x²(czarny wykres ) że jej wykres jest przesuniety o jedna jednostke w dól Nie ma to zadnego wplywu na jej roznowatosciowosc Więc tak jak g(x)=x²−1 nie ma funkcji odwrotnej to takze y=x² tez nie bedzie miała funkcji odwrotnej jesli rozpatrujemy naturalna dziedzine Teraz funkcja f(x)=log₂(x+1) Dziedzina jej =.............. Zbior wartosci =.................. podaj to

Butek: https://ibb.co/PGK0Qq1

q: Odpowiedzi na pytanie z 12:15 nie ma a piszesz o całym dniu .No ale... D(f)=(−1,∞) ZW(f)= (−∞,∞) Funkcja jest roznowartosciowa −mozesz to wykazac i na Funkcja odwrotna do funkcji logarytmicznej jest funkcja wykladnicza f{−1}=2^x−1 ========================================= Ogolnie O funkcji h mowimy ze jest superpozycja (albo zlozeniem ) funkcji f i g i oznaczamy symbolem h=fog W tym przypadku mamy Zw(g)⊂D(f) Inaczej to dziedzina funkcji f musi zawierac zbior wartosci funkcji g natomiast jesli mamy zlozenie h=gof to w tym przypadku mamy Zw(f)⊂D(g) Inaczej przy tym zlozeniu dziedzina funkcji g musi zawierac zbior wartosci funkcji f f(x)= log₂(x+1) D(f)=(−1,∞) Zw(f)=ℛ=(−∞,∞) g(x)= x²−1 D(g)=ℛ=(−∞,∞) Zw(g)=<−1.∞) Teraz patrz czy mozesz zrobic zlozenia h=fog i h=gof Dobranoc

q: Może żeby nie było kolizji oznaczeń to oznacz tak h=fog i k=gof aby pokazać ze s a to inne złozenia Mozesz sie tez spotkać z takim zapisem h=fog albo h(x)=f(g(x)) k=gof albo k(x)=g(f(x))

jc: Pomyliłem literę, y=f(x), x=f⁻¹(y). Przy okazji, oznaczenia D(f), Zw(g) spotyka się chyba tylko w szkole. W teorii kategorii widziałem dom(f), cod(f). Być może po prostu uczyłem się z podręczników, których autorzy bardzo oszczędnie stosowali symbolikę matematyczną.

chichi: dom(f) i rng(f), od domain i range − stosowane w teorii mnogości

q: Tak jc oznaczenia ze szkoly.

q: https://zapodaj.net/plik-emKhVB77jg

q: Te zadania które sa na dole to zadania dla maturzystów i kandydatów na wyższe uczelnie Postaraj sie to zadanie zrobic