rozwiaz w zbiorze liczb zespolonych artdeco: z³ = (√3 + i ) / (2−2i) jak do tego podejsc?

ABC: pomnożyć przez sprzężoną a potem układ równań rozwiązać

ABC: albo ze wzoru pierwiastkowego

Adamm: Wzór de Moirve'a

artdeco: co masz na mysli przemnozyc przez sprzezona (a −bi)

Adamm: Zapisujemy prawą stronę w postaci eksponencjalnej lub trygonometrycznej z³ = r*exp(iφ) z = ³√r*exp(i(φ+2πk)/3) dla k = 0, 1, 2

artdeco: a to czegos takiego w ogole nie mialem

artdeco: a jesli chodzi o ten wzor na potege zⁿ = I z I ² ( cos n α + i sin α) to co mam tu podstawic w tym dziwnym rownaniu?

Adamm: exp(iφ) = cos(φ) + i sin(φ) Kwestia zapisu tak naprawdę, chociaż może widać lepiej skąd te wzory się biorą

artdeco: ja nie wiem o czym ty piszesz nie znam exp czy da sie obliczyc to z tego wzoru co podalem albo tego drugiego na pierwiastek?

6latek:

√3+i		2+2i
	*		Przemnoz i uporzadkuj do postaci a+bi
2−2i		2+2i

potem liczysz pierwiastki stopnia trzeciego z tej liczby Widzisz analogie do poprzedniego zadania ?

artdeco: z³ = ( (√3 − 1) / 4 + (( (√3 + 1) / 4 )i i co dalej?

6latek: Podstawiaj do wzoru Postac trygonometryczna i jedziesz

artdeco: do wzoru?

6latek: masz wzor na pierwiastkowanie liczb zespolonych Patrz co tam potrzeba i licz

artdeco: no ale tam jest z³ jak to niby podstawic? _n √IzI (cos (( α +2kπ) / n) ) + isin (α + 2kπ) / n ) nie rozumiem niby jak tego tu uzyc

6latek: najpierw liczbe (√3−1)/4+i(√3+1)/4 sprowadz do postaci trygonometrycznej

artdeco: z = IzI (cosα + isinα) jak?

6latek: tak

artdeco: no ale jak ja mam niby takie cos z ulamkami zapisac pod ta postacia?

6latek: ale jaki widzisz w tym problem ? |z|= √a²+b² a=(√3−1)/4 to a²= (√3−1)²/4²= licz b²= √3+1)/4 to b²=(√3+1)²/4² potem sobie wstawiasz a²−b² pod pierwiastek i wyznaczasz moduł

artdeco: no i to wyjdzie jakies szalenstwo poza tym jak wyznacze te katy

6latek: To sa podstawowe wzory

	a		an
(		)n=
	b		bn

potem wstawiasz a² i b² pod pierwiastek ma byc

6latek: To co ja mam ci liczyc ? nawet nie probujesz tylko od razu narzekasz

artdeco: IzI = P{2} / 2 ale jak mam wyznaczyc te katy potrsebne do wzorow

artdeco: √2 /2 mialo byc

artdeco: policzylem ten sinus i cos i o ile dobrze mi wyszlo to cos α = 2− √3 sinα = (√6 + √2) / 4

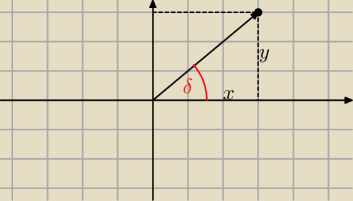
6latek: zapisze sobie tak z=x+yi Nasza liczba bedzie lezała w 1 cwiartce

	√3−1
x=		>0
	4

	√3+1
y=		>0
	4

więc albo liczysz tak

	y
sinφ=
	|z|

	x
cosφ=
	|z|

albo mozesz tez policzyc ten kąt z tangensa .Patrz na rysunek

	y
Zobacz ze tgδ=
	x

Wiec my mozemy u siebie zapisac ze

	√3+1
tgφ=		= policz i sprawdz w tablicach dla jakiego kata ten tangens jest równy
	√3−1

6latek: Jesli policzyles sinα i cosα to sprawdz w tablicach bo to nie bedzie 30^o,60^o 45^o

artdeco: cos kolo 15 stopni

artdeco: a nie

artdeco: tgφ = 2 + √3

artdeco: jak to niby sprawdzic

6latek: tgφ=2+√3 to φ=75^o

√6+√2
	=cos15o
4

sin(90^o−α)= cosα stad sin75^o=cos15 ^o czyli nasze φ=75^o

6latek:

	5
φ=75o=		π
	12

Teraz tylko podstawiaj do wzoru na pierwiastki

artdeco: z = √2 / 2 ( cos 5/12 π + i sin 5/12 π)

artdeco: ( √3 − 1 + i + i√3 ) / 4

6latek: No to jedziesz z₀= z₁= z₂=

artdeco: i to cos to jest pierwiastek?

6latek: Tu bedziesz miał 3 pierwiastki nie jeden

artdeco: ze ze wzoru na potege?

artdeco: z = IzI (cosα + isinα) nie z tego?

6latek: Nie z tego Ze wzoru na pierwiastki zapis z³=cos tam oznacza tyle ze musisz znależć taką liczbe z ktora podniesiona do potegi trzeciej da to cos tam

6latek: Masz taka sytuacje x³=64 x=³√64=4 bo 4³=64

artdeco: zⁿ = IzIⁿ (cos n α + isin n α) o tym mowisz?

6latek: Napisałem CI ze wzor na pierwiastki zespolone a nie na potegowanie

artdeco: wk=( (cos(φ+2kπ)/n) +isin (φ+2kπ)/(n) , k=0,1,…,n−1. o to chodzi?

artdeco: i tam przed jeszcze ten pierwiastek z IzI n stopnia

6latek: A i owszem

artdeco: pod n we wzorze mam podstawiac 3 tak bo 3 potega?

6latek: tak

artdeco: https://ibb.co/m65F86D Wyszły mi takie. Ja mam to tak zostawic?

jc: To na prawdę dało się napisać tu, a nie na nieczytelnym zdjęciu. argument = 5π/12 moduł = 1/√2 rozwiązanie ma moduł = 2^−1/6 i argumenty: 5π/36, 5π/36 + 2π/3, 5π/36 + 4π/3

jc: A co chciałbyś jeszcze z tym zrobić?

artdeco: Ale skąd ci wyszły te 5/36 π ₃ z0 = √ (√2 ) / 2 ( cos 5/36 π + I sin 5/36 π ) Mi tak wyszło tam na zdjęciu na jednym z 3

6latek: Ty tak naprawde czy nie wiesz?

6latek: Komentarz po tym co napisze zostawie Tobie

5π		5π		1		5π
	:3 =		*		=
12		12		3		36

artdeco: Ale po co pokazujesz jak się dzieli

artdeco: Pokazuje ci równanie które mi wyszło z pierwiastkiem sin I cos I pytam czemu to wszystko wyrzucacie i zostawiacie sam Kat

6latek: Pytasz skąd wyszlo ? Pokazuje . Skoro wiesz to po co pytasz? Po drugie zobacz ja wstawiasz . Głowa mi się skręci zanim odczytam . Czy naprawdę nie potrafisz wykonać tak prostych działań ? Przecież jeśli k=0 to 2kπ=2*0*π=0 a 0/3=0 stąd sam kat . Czy naprawde musisz o to pytac ? Wybacz ,ale śmieszno i straszno .

artdeco: Moja wiadomość z 20;40 gdzie tam ci zostaje sam kat? To jest przypadek dla z0

6latek: Inaczej jc napisał Ci tylko argumenty które stawiasz przy cosinusie i sinusie dla z₀,z₁ i z₂

artdeco: no o to pytam. Czyli odpowiedź to jest ta całość z cos sin itp

6latek: Czy teraz juz wszystko jasne ? Należalo wziąc na początek jakiś prosciejszy przykład i go zrobic Potem dopiero trudniejszy .Od godz 14:30 z przerwami do prawie tej pory zeszło Teraz policz np z³=1

Mila: i²=−1

	√3 + i		(√3+i)*(2+2i)
z3 =		*
	(2−2i)		22+22i2

	1
z3=		(1+i)*(√3+i)
	4

	1		π		π		π		π
z3=		*√2(cos		+i sin		)*2*(cos		+i sin		)
	4		4		4		6		6

	√2		5π		5π
z3=		*(cos		+i sin		)
	2		12		12

√2		1
	=
2		√2

	1		5π		5π
z0=		*(cos		+i sin		=
	6√2		3*12		3*12

	1		5π		5π
=		*(cos		+i sin		)
	6√2		36		36

	1		5π   +2π 12		5π   +2π 12
z1=		*(cos		+i sin		)
	6√2		3		3

	1		5π   +4π 12		5π   +4π 12
z2=		*(cos		+i sin		)
	6√2		3		3

dokończ obliczenia w z₁ i z₂

artdeco: Ten kolejny wpis pokazuje jakiś błąd w poprzednich moich rozwiązaniach czy co to wnosi

Mila: Ja mam błąd w pierwszym zapisie z³. Tam miał być znak równości zamiast mnożenia. Źle widać w tym edytorze, a nie włączyłam podglądu. Ma być:

	(√3+i)*(2+2i)
z3=
	(2−2i))*(2+2i)

dalej dobrze

6latek: Dobry wieczór Milu Sposób rozwiązania rozumiem napisz jesli możesz jak rozbiłas ta liczbe po prawej stronie (bez tej 4 ) na (1+i)(√3+i)

Mila: Jutro Ci dokładnie rozpiszę. Dobranoc

6latek: Dobranoc

Mila: cd. 22: 52

	(√3+1)*2*(1+i)
z3=
	22−22*i2

	2*(√3+1)*(1+i)
z3=
	8

i dalej jak napisane 22:30

6latek: Sliczne dzięki Milu Dalej wiem o co chodzi