geometria aksjomat: Przez wierzchołek C trójkąta ABC prowadzimy dowolną prostą l. Niech P, Q będą rzutami wierzchołków A, B na prostą l oraz niech M będzie środkiem boku AB . Wykaż, że M P = MQ

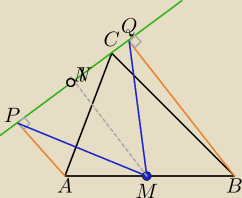
Mila: Podpowiedź : Czworokąt PABQ− trapez prostokątny MN − odcinek łączący środki ramion

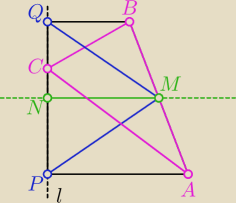
chichi: prowadząc prostą równoległą do prostych AP oraz BQ przecinamy prostą l w punkcie N. z oczywistych względów |NP| = |QN| → ΔQMP jest równoramienny, zatem |MQ| = |MP| □

chichi: o i pojawiło się w trakcie pisania...

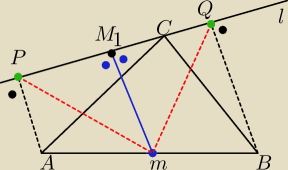
6latek: Skoro punkty P i Q sa rzutami to znaczy ze |PQ|=|AB| Stad takze punkt M₁ jest srodkiem odcinka PQ więc |PM₁|= |M₁Q| MM₁ pada pod kątem prostym na prostą l więc jest wysokościa trojkąta PMQ Wiemy ze albo w trójkącie rownobocznym albo w trojkącie rownoramiennym wysokośc dzieli podstawe na polowy Więc ΔPMQ jest takim trójkątem Z tego mamy ze PM=QM