omj świrek: hej, czy uważacie, że omj część korespondencyjna była trudna w tym roku? czy łatwa? (skończyła się już)

wredulus_pospolitus: a wrzuć link do zadań

świrek: https://omj.edu.pl/uploads/attachments/19omj-1etap.pdf

wredulus_pospolitus: Tak szybko patrząc. Dla 'typowego ucznia' zadania 4, 5, 6 powinny być rozwiązywalne. Dla 4−5'wego ucznia zadanie 2 i 3 powinno być rozwiązywalne. Zadanie 1 i 7 mogłyby sprawić jakieś większe problemy, ale tylko dlatego, że w szkołach nie uczą nas 'kombinować'

świrek: ja wysłałam wszystkie (zobaczymy z jakim skutkiem)

świrek: najłatwiejsze moim zdaniem były zadania nr 1 oraz nr 7 najtrudniejsze moim zdaniem było zadanie nr 3

wredulus_pospolitus: To jaki Ci kąt wyszedł w '2'

wredulus_pospolitus: No to dajesz 3 ... jakie typy liczb powstawały z zapałek

świrek: chyba 135

wredulus_pospolitus: nawet na pewno 135

świrek: n≥8 w trzecim (wykazałam to)

wredulus_pospolitus: nie zrozumiałaś mnie ... w (3) zadaniu powstają konkretne liczba dla n = 2k i konkretna liczb dla n=2k+1 Jakie to liczby

świrek: nie rozumiem:( jeśli n=2k no to np. 44, 66, 454 jeśli n=2k+1 no to np. 45, 65

wredulus_pospolitus: nie dla 1 zapałki − brak liczby dla 2 zapałek mamy liczbę '1' suma 1 dla 3 zapałem mamy liczbę '7' suma 7 dla 4 zapałek mamy liczbę '11'' suma 2 dla 5 zapałek mamy liczbę '71' suma 8 dla 6 zapałek mamy liczbę'111' suma 3 dla 7 zapałek mamy liczbę '711' suma 9 dla 8 zapałek mamy liczbę'1111' suma 4 dla 9 zapałek mamy liczbę '7111' suma 10 dla 10 zapałek mamy liczbę'11111' suma 5 itd. widzisz jak powstają NAJWIĘKSZE możliwe liczby Oto mi chodziło

świrek: no używamy liczb, które składają się z najmniejszej liczby zapałek, czyli 1 i 7

wredulus_pospolitus: więc mamy dwie możliwości: dla n= 2k mamy liczbę której suma cyfr będzie równa k dla dowolnego k>0 zachodzi n = 2k > k <−−− czyli te liczby nigdy nie spełnią warunki zadania dla n = 2k+1 mamy liczbę której suma cyfr będzie równa (k−1) + 7 = k+6 i teraz −−− kiedy n = 2k+1 = k+6 i masz rozwiązanie

wredulus_pospolitus: Tylko jeszcze dopowiem −−− to co napisałem o 18:32 sprowadza się do uczniów klasy 8 niższe klasy niestety nie mają odpowiedniej wiedzy (znajomość wzorów) do rozwiązania zadań 4,5

świrek: 11

świrek: no ja jestem w ósmej klasie

wredulus_pospolitus: no dobrze ... zad 1 i 7 −−−− musiałbym pomyśleć nad tym, więc zostawmy to na później. 4. jak zrobiłaś

świrek: y³−x³=p (y−x)(y²+xy+x²)=p jedno z tego jest równe 1, ponieważ p to liczba pierwsza (x i y też) ten drugi nawias nie może być 1, bo to są całkowite więc ten drugi y−x=1 y=x+1 więc jedna z nich parzysta jeśli y=2 (2 to jedyna parzysta pierwsza liczba) to x=1 niemożliwe czyli x=2 y=3 no i wszystko się zgadza 27−8=19 koniec

świrek: widziałam jak ktoś kiedyś rozwiązywał takim sposobem na forum

świrek: ale oczywiście to rozwiązanie, które widziałam kiedyś było opublikowane przed konkursem

wredulus_pospolitus: Ok 5 zadanie −−− to kwestia narysowania przekątnej prostokąta i użycie tw. Pitagorasa aby zobaczyć, że: r₁² = r₃² − r₂² a następnie napisać wzory na pola i mamy równość

świrek: ok dzieki

wredulus_pospolitus: 6. także raczej nie mam co pytać. no dobra ... to jak podeszłaś do zad 1

świrek: w pierwszym zadaniu to jak n>1 to liczba jest podzielna np. n=2, czyli 1199 przez 11 n=3, czyli 111999 przez 111 itd. ja to wykazałam, że gdy n>1 to liczba nie jest pierwsza czyli n=1 to wtedy 19 i jest pierwsza

wredulus_pospolitus: masz rację a ostatnie .. 7

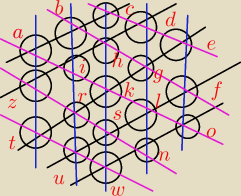
świrek: suma wszystkich okienek 11+12...+29=380 380/5=76 c+d+e=b+h+g+f=a+i+k+l+o=z+r+s+n=t+u+w=76 c+d+e+b+h+g+f+a+i+k+l+o=228=3*76 (a+b+c)+(e+f+o)+i+k+l+h+g+d=228 2x76+i+k+l+h+g+d=228 i+k+l+h+g+d=76 to niemożliwe ponieważ nawet biorąc 11,12,13...,16 czyli pierwsze sześć ze zbioru A={11,12...,29} suma liczb 11+12+13+14+15+16>76

wredulus_pospolitus: okey

wredulus_pospolitus: no to widać, raczej dobrze Ci poszło −−− chyba tylko to z zapałkami Ci nie poszło, albo po prostu się nie zrozumieliśmy.

świrek: wydaje mi się, że to trzecie zadanie dobrze zrobilam, bo długo nad nim siedziałam, moze jest faktycznie tak jak piszesz jak coś się dowiem to dam znać (jeśli nie zapomnę oczywiście)

świrek: @wredulus zamieścili dzisiaj rozwiązania faktycznie z patyczkami źle (nie zrozumiałam polecenia hehe)

wredulus_pospolitus: Nie przejmuj się z tymi patyczkami −−− ja w pierwszej chwili myślałem o tym, że będą tworzone '9' (jak tylko mamy wielokrotność 6 patyczków) i dopiero po jakimś czasie (gdy zacząłem się przyglądać sprawie dokładniej − czyli zacząłem wypisywać jak to wygląda od najmniejszych n) dotarło do mnie, że przecież 11 > 9 a zużywam mniej patyczków Tak czy siak − mam nadzieję, że czujesz się dumna z tego, że rozwiązałaś tyle zadań i rozwiązałaś je prawidłowo. Moje gratulacje.

świrek: Dziękuję. To przecież bardzo prestiżowa olimpiada. Odpowiednik OM Mam nadzieję, że te zadania z wykazywaniem były dobrze