proszę o rozwiązanie anna: oblicz sumę dziesięciu najmniejszych dodatnich pierwiastków równania 2sin²x =1 ja to wykonałam tak 2sin²x =1 sin²x =¹₂ sinx = ^√2₂ x = ^π₄ + 2kπ k∊ Z x = a₁ = ^π₄ a₂ = ^π₄ + 2*2π = ¹⁷₄π r= ¹⁷₄π − ^π₄ =4π a ₁0 = ^π₄ + 9*4π =^145π₄ czyli S₁₀ =(( ^π₄ + ^145π₄)/2)*10 = wynik jest 25π

wredulus_pospolitus:

	√2
a czemu odrzucasz: sinx = −		to 'x' (pierwiastek) ma być >0 ... a nie wartość
	2

sinx

wredulus_pospolitus:

	π		√2
kolejna sprawa −−− x =		+ 2kπ to nie jedyne 'x' dla których sinx =
	4		2

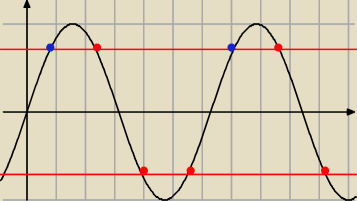
Ty masz jedynie niebieskie punkty a co z czerwonymi

Aruseq: Po pierwsze: brakuje rodziny rozwiązań x=^3π₄+2kπ Po drugie: twoje a₁ to rzeczywiście ^π₄, ale a₂ to będzie ^π₄+2π, a nie +4π

wredulus_pospolitus:

	π
alternatywna droga: 2sin2x = 1 −−−> 2sin2x − 1 = 0 −−−> cos(2x) = 0 −−−> 2x =		+ kπ
	2

	π		kπ
−−−> x =		+		−−− i teraz będą wszystkie punkciki wzięte pod uwagę
	4		2

anna: jeżeli a₁=^π₄ a₂ =^π₄+π= ³₄ r = ¹₂π a₁₀= ^π₄ +9* ¹₂π = ^π₄ +⁹₂π = ¹⁹₄π S₁₀ =(( ^π₄ + ¹⁹₄π )/2)10 =25 czy to jest poprawne

wredulus_pospolitus: Wyszło Ci 25π ... i taka napisałaś że jest odpowiedź ... pomijając błędy zapisu ... powinno być dobrze

anna: dziękuję bardzo