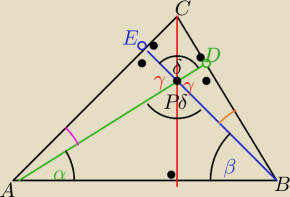
Trójkat i wysokości Krzysiek: W ostrokątnym trójkącie ABC wysokości przecinają się w punkcie P Mając dane kąt |BAP|=α i kąt |ABP|=β oblicz miary kątów trójkata ABC W trójkącie APB miara ∡|APB|=δ= 180^o−(α+β) Stąd miara kąta |EPD| wynosi także 180^o−(α+β) jako kąty wierzchołkowe ∡|ECD|=360^o−[2*90^o−180−(α+β)]=α+β W trójkącie ACD ∡|CAD|= 90^o−(α+β)=90^o−α−β ∡|CAB|=90^o−α−β+α= 90^o−β W trójkącie CEB ∡|EBC|=90^o−(α+β) ∡|ABC|=90^o−(α+β)+β= 90^o−α Kąty trójkata ABC maja miare (α+β) , 90^o−α, 90^o−β

wredulus_pospolitus: Alternatywnie: 1. ΔADB −−−> masz kąt 90−α (pierwszy kąt załatwiony) 2. analogicznie ΔAEB −−−> masz kąt 90−β (drugi kąt załatwiony 3. i w końcu ΔABC −−−> masz kąt (α+β) −−− i po krzyku

Krzysiek: Tak prościej Może trochę dłużęj ale sobie tak rozumuję . dzięki