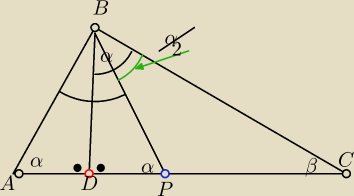
trójkat prostokatny Krzysiek: W trójkącie ABC z wierzchołka B kata prostego poprowadzono wysokość BD i dwusieczną BP kąta DBC. Okazało się że |AB|=|BP| Oblicz miary kątów trójkąta ABC i wykaż że bp jest jego środkową Dla trójkąta ABP

	α
α+α+(90−		)=180o
	2

4α−α=180^o 3α=180^o α=60^o β=30⁰ trójkąt ABC ma kąty równe 90^o,60^o,30^o Kąty mam teraz wykazać że BP jest środkową czyli |AP|=PC| Myslę to zrobić tak Trójkąt ABP to trójkąt równoboczny więc |AB|=|BP|=|AP| Trójkąt BPC jest trójkątem równoramiennym stąd |BP|=|PC| Skoro |BP|=|AP| i |BP|=|PC| to BP jest jego środkową

chichi:

	90o
skoro BP − dwusieczna, to |∡ABP| =		= 45o, to po ile będą miały α
	2

wredulus_pospolitus: Alternatywne podejście ∡ABD = ∡BCD (z sumy trójkątów prostokątnych o jednym z kątów równym α)

	α
Dodatkowo ∡ABD =
	2

stąd:

3		90o
	α = 90o ∧ β =
2		3

Stąd mamy, że ΔABP jest równoboczny, a ΔBCP jest równoramienny

wredulus_pospolitus: @chichi −−− dwusieczna ale nie ∡ABC tylko ∡DBC

chichi: ahhh.. nie doczytałem, przeskoczyło do następnego wiersza. racja

Krzysiek: chichi W pierwszym momencie zrobiłem rysunek taj jak piszesz i zastanawiałem sie jak to możliwe