czworokat
Krzysiek:
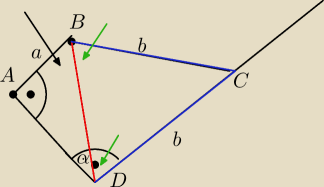
W czworokącie kąty przy wierzchołkach A i D sa proste i |BC|=|CD|.
Wykaż że w prostej BD zawarta jest dwusieczna kąta B
W trójkącie ADB kąt |ABD|=90
o−α
W trojkącie równoramiennym BCD kąt |BDC|=90
o−α i równy jest kątowi DBC
Stąd ∡|ABD|=∡|DBC| wiec prosta BD jest dwusieczna kąta przy wierzchołku B
7 paź 22:11
wredulus_pospolitus:
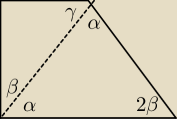
1. Ze względu na kąty proste −−−> mamy tutaj trapez prostokątny o podstawach AB i DC.
2. ΔBCD jest równoramienny −−−> stąd kąty α
3. oznaczamy kąt β = 90
o − α −−−> stąd kąt przy wierzchołku C (równy 180
o − 2α) jest równy
2β
4. z sumy kątów w trapezie: 180
o = 2β + α + γ −−−> 180
o = 180
o − 2α + α + γ −−−> α = γ
7 paź 22:18
wredulus_pospolitus:
alternatywne rozwiązanie
Rysunek identyczny, tylko nie zaznaczamy kąta 2β i olewamy fakt, że jest to trapez
1. ΔBCD jest równoramienny −−−> stąd kąty α
2. oznaczamy kąt β = 90o − α
3. z Sumy kątów w trójkącie prostokątnym ABD mamy: γ = 180o − (90o + β) = α
c.n.w.
7 paź 22:19
Krzysiek:
Dzięki serdeczne

7 paź 22:23
Krzysiek:
W pierwszym momencie przyszedł mi na myśl kwadrat wiec sprawa prosta
Ale potem no nie może być tez inny czworokąt
7 paź 22:25
dwusieczna:
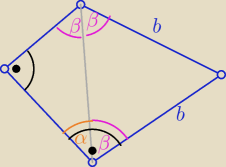
7 paź 22:45
Krzysiek:

7 paź 23:14
 W czworokącie kąty przy wierzchołkach A i D sa proste i |BC|=|CD|.
Wykaż że w prostej BD zawarta jest dwusieczna kąta B
W trójkącie ADB kąt |ABD|=90o−α
W trojkącie równoramiennym BCD kąt |BDC|=90o−α i równy jest kątowi DBC
Stąd ∡|ABD|=∡|DBC| wiec prosta BD jest dwusieczna kąta przy wierzchołku B
W czworokącie kąty przy wierzchołkach A i D sa proste i |BC|=|CD|.
Wykaż że w prostej BD zawarta jest dwusieczna kąta B
W trójkącie ADB kąt |ABD|=90o−α
W trojkącie równoramiennym BCD kąt |BDC|=90o−α i równy jest kątowi DBC
Stąd ∡|ABD|=∡|DBC| wiec prosta BD jest dwusieczna kąta przy wierzchołku B
 1. Ze względu na kąty proste −−−> mamy tutaj trapez prostokątny o podstawach AB i DC.
2. ΔBCD jest równoramienny −−−> stąd kąty α
3. oznaczamy kąt β = 90o − α −−−> stąd kąt przy wierzchołku C (równy 180o − 2α) jest równy
2β
4. z sumy kątów w trapezie: 180o = 2β + α + γ −−−> 180o = 180o − 2α + α + γ −−−> α = γ
1. Ze względu na kąty proste −−−> mamy tutaj trapez prostokątny o podstawach AB i DC.
2. ΔBCD jest równoramienny −−−> stąd kąty α
3. oznaczamy kąt β = 90o − α −−−> stąd kąt przy wierzchołku C (równy 180o − 2α) jest równy
2β
4. z sumy kątów w trapezie: 180o = 2β + α + γ −−−> 180o = 180o − 2α + α + γ −−−> α = γ


