Pięciokąt foremny
Krzysiek:
Punkty A,B,C,D,E są wierzchołkami pięciokąta foremnego
Wykaż że punkty przecięcia się jego przekątnych są również wierzchołkami pięciokąta foremnego
We wskazówce do zadania jest napisane żeby wykazać że kąty nowo powstałego pięciokąta są równe
|AE|=|ED|=|DC|=|CB=|BA|
Stąd trójkąty ABE, AED, DCB, CBA sa rownoramienne i mają równe kąty α przy podstawach i równe
podstawy BE=AD=DB=AC
czy należy napisać jeszcze że kąty |PAT| , |SET|, |SDR|, ||RCQ|. |QBP| też są równe i mają
miare 108
o−2α, gdyz kąt wewnętrzny pięciokąta foremnego ma miare 108
o
Wobec tego trójkaty ATE, ESD, DRC,CQB BPA też są równoramienne o kącie przy wierzchołkach
180
o−2α
Stąd miara kątów |PTS|, |TSR|, |SRQ|. |RQP|i |QPT| też jest równa 180
o−2α jako kąty
wierzchołkowe
Kąty powstałego wielokata są równe wiec powstały pięciokąt tez jest pięciokątem foremnym
wredulus_pospolitus:
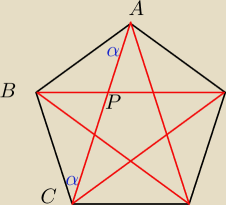
ΔACB jest równoramienny stąd mamy kąty
α
w pozostałych miejscach uzupełniamy poprzez analogię (jako że mamy trójkąty przystające − cecha
BBB)
zauważmy, że ΔABP jest równoramienny (analogiczne pozostałe − znowu przystające trójkąty)
oznaczmy |AP| = x oraz |AC| = y
wtedy |PQ| = |PT| = |TS| = |SR| = |QR| = |AC| − 2|AP| = y − 2x
c.n.w.
Dzięki . Przystawanie trójkątów mam w zbiorze w następnym rozdziale
