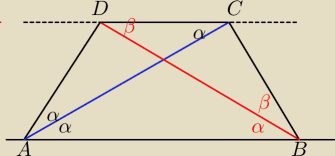
Trapez Krzysiek: Wykaż że jeśli przekątne trapezu zawierają sie w dwusiecznych kątów leżących przy jednej z podstaw to trzy boki tego trapezu maja takie same długości Trójkąty ADC i DCB to trójkąty równoramienne Teraz żeby udowodnić to twierdzenie to należy wykazac że ∡α=∡β Myśle tak ΔADC i ΔDCB maja wspołne ramię DC. Skoro tak to AD=DC i DC=CB Z tego wynika że skoro oba trójkąty mają równe ramiona to kąty przy podstawie AC trójkąta ADC i kąty przy podstawie DB trójkąta DCB są rowne −czyli α=β

wredulus_pospolitus: A skąd to czerwone α Na jakiej podstawie założyłeś na początku to co później próbujesz wykazać

wredulus_pospolitus: Druga sprawa −−− nie musisz udowodnić, że α = β "ΔADC i ΔDCB maja wspólne ramię DC" na tym powinien się kończyć Twój dowód (skoro mają wspólne ramię, a są to równoramienne, to |AD| = |DC| = |CB| −> c.n.w.)

Krzysiek: To pomyłka . Mialobyc β bo to dwusieczna kata Ale może tak być?

wredulus_pospolitus: może być ... ale że to za długo Po prostu już krok wcześniej to wykazałeś Nawet to napisałeś: "AD=DC i DC=CB" w trzeciej od końca linijce. Więc dwie ostatnie linijki są zbyteczne

Krzysiek: Dobrze . dziękuje