
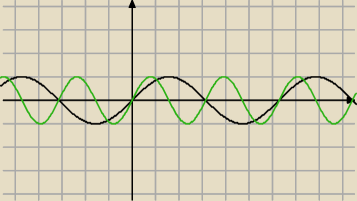
 y=sin(x) czarny
y=sin(2x) zielony
Możesz pokazać swoje rozwiążanie?
y=sin(x) czarny
y=sin(2x) zielony
Możesz pokazać swoje rozwiążanie?
| 3 | ||
sin(2x)=sin | π+2kπ gdzie k∊C | |
| 2 |
| 3 | ||
2x= | π+2kπ | |
| 2 |
| 3 | ||
x= | π+kπ i k∊C | |
| 4 |
| 1 | ||
jeśli k=−1 to x= 0,75π−π= −0,25π= − | π itd | |
| 4 |
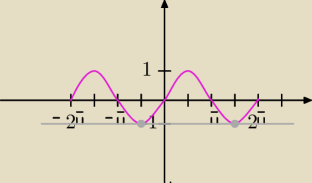 ja rozrysowałem to tak i wyszło mi że linia przechodzi przez punkt −π2 i 3π2
wtedy 2x= −π2 + 2kπ i 2x= 3π2 + 2kπ
i po podzieleniu na 2 wyszło mi x= −π4 + kπ i x= 3π4 + kπ
ale teraz zauważyłem, że tak naprawdę to jest to samo i jeśli rozważę np. przedział od 0 do 2π
to mam tylko jeden punkt więc powinien być jeden wynik.
Popraw mnie proszę jeśli źle to rozumiem ale wydaje mi się, że można napisać albo x= −π4+
kπ albo x= 3π4 + kπ i oba wyniki będą poprawne bo to jeden powtarzający się punkt
ja rozrysowałem to tak i wyszło mi że linia przechodzi przez punkt −π2 i 3π2
wtedy 2x= −π2 + 2kπ i 2x= 3π2 + 2kπ
i po podzieleniu na 2 wyszło mi x= −π4 + kπ i x= 3π4 + kπ
ale teraz zauważyłem, że tak naprawdę to jest to samo i jeśli rozważę np. przedział od 0 do 2π
to mam tylko jeden punkt więc powinien być jeden wynik.
Popraw mnie proszę jeśli źle to rozumiem ale wydaje mi się, że można napisać albo x= −π4+
kπ albo x= 3π4 + kπ i oba wyniki będą poprawne bo to jeden powtarzający się punkt
