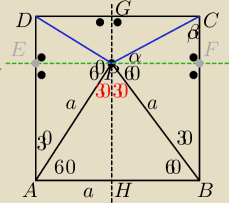
 Wierzchołek P trójkata równobocznego ABP jest punktem wewnętrznym kwadratu ABCD
Oblicz miary kątów BPC, CPD, DPA
|AB|=a
Wierzchołek P trójkata równobocznego ABP jest punktem wewnętrznym kwadratu ABCD
Oblicz miary kątów BPC, CPD, DPA
|AB|=a
| a√3 | ||
|PH|= | ||
| 2 |
| a√3 | ||
|GP|=|CF|=a− | ||
| 2 |
| 2a−a√3 | a(2−√3) | |||
|GP|= | = | |||
| 2 | 2 |
| |PF| | ||
tgβ= | = (1/2a)/[a(2−√3)/2]=2+√3 | |
| |CF| |
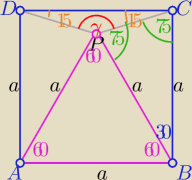 ΔBPC równoramienny o kątach .....
γ= 360o−2*75o−60o
γ=150o
i po ptokach
ΔBPC równoramienny o kątach .....
γ= 360o−2*75o−60o
γ=150o
i po ptokach 
 Ptoki ,ptokami ale teraz widzę że można to było zrobić prościej
Dziękuje .
Mam jeszcze takie pytanko.
Jest zadanie z trapezem (tez obliczyć kąty )
Jeśli trapez ma 3 boki równe to musi być na bank równoramienny ?
Ptoki ,ptokami ale teraz widzę że można to było zrobić prościej
Dziękuje .
Mam jeszcze takie pytanko.
Jest zadanie z trapezem (tez obliczyć kąty )
Jeśli trapez ma 3 boki równe to musi być na bank równoramienny ?
