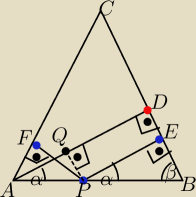
Na podstawie AB trójkąta równoramiennego ABC obrano dowolny punkt P .
mamy wykazać że suma odległośći punktu P od ramion AC i BC jest równa długości wysokości
trójkąta poprowadzonej z wierzchołka A
Mamy więc udowodnić że|FP|+|PE|= |AD|
AD i PE padają pod tym samym kątem na bok BC więć sa równoległe stąd |PE|=|QD|
Teraz należąloby wykazac że |AQ|=|FP| i mamy teze
Jeżeli udałoby sie wykazać ze Δ FAP≡ΔAPQ to po zadaniu
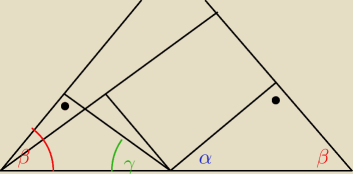Z podobieństwa trójkątów (KKK) mamy : α = γ
w takim razie ΔAQP przystaje do ΔPFA (kbk)
