Punkt wewnątrz czworokąta
Krzysiek:
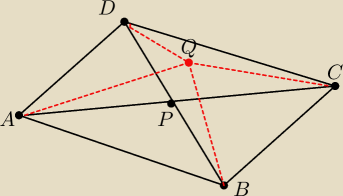
Znajdz taki punkt wewnątrz danego czworokąta wypukłego aby suma odległości od wierzchołków
czworokąta była najmniejsza
Punkt P przecięcia sie przekątnych czworokąta ABCD będzie tym punktem wewnątrz danego
czworokąta dla którego suma odległości od wierzchołków czworokąta bedzie najmniejsza
Obieram sobie inny punkt Q który leże wewnątrz czworokąta
Musze udowodnić że
|AP|+DP|+|PC|+|PB|<|AQ|+DQ|+|CQ|+|BQ|
Mam że |AP|+|PC|+DP|+|PB|=|AC|+|DP| czyli długości obu przekątnych
Jesli P≠Q to mam 3 możliwości
1) Q∊AC
2) Q∊BD
3) Q∉AC i także Q∉BD
Dla nr 1
|AQ|+|QC|=|AC| i |BQ|+|QD|>|BD|
Dla nr 2
|DQ|+|QB|=|DB| i |AQ|+|QC|>|AC|
Dla nr 3
|AQ|+|QC|>|AC| i |DQ|+|QB|>|DB|
Widzę że w każdej tej możliwości
|AQ|+|QC|+|DQ|+|QB|>|AP|+|PB|+|CP|+|DP|
Więc punkt P jest tym jedynym punktem który spełnia warunki zadania .
I to by mi się zgadzało z rozwiązaniem i to jest prawidłowe rozumowanie jakie chciał autor
zadania .
Jednak autor zadaje dodatkowe pytanie . Czy potrafisz wskazać gdzie skorzystałeś z tego ze
czworokąt jest wypukły ?
A jakie to ma znaczenie czy jest wypukły czy wklęsły bo naprawdę nie wiem ?
3 paź 17:16
Krzysiek:
Ktoś może odpowie?
3 paź 19:13
Krzysiek:
4 paź 18:19
ABC:
definicja wypukłości − odcinek łączący dwa dowolne punkty figury jest CAŁY zawarty w tej
figurze
4 paź 18:24
Krzysiek:
No tak.
Rzeczy oczywiste . Dziękuje

4 paź 18:29
 Znajdz taki punkt wewnątrz danego czworokąta wypukłego aby suma odległości od wierzchołków
czworokąta była najmniejsza
Punkt P przecięcia sie przekątnych czworokąta ABCD będzie tym punktem wewnątrz danego
czworokąta dla którego suma odległości od wierzchołków czworokąta bedzie najmniejsza
Obieram sobie inny punkt Q który leże wewnątrz czworokąta
Musze udowodnić że
|AP|+DP|+|PC|+|PB|<|AQ|+DQ|+|CQ|+|BQ|
Mam że |AP|+|PC|+DP|+|PB|=|AC|+|DP| czyli długości obu przekątnych
Jesli P≠Q to mam 3 możliwości
1) Q∊AC
2) Q∊BD
3) Q∉AC i także Q∉BD
Dla nr 1
|AQ|+|QC|=|AC| i |BQ|+|QD|>|BD|
Dla nr 2
|DQ|+|QB|=|DB| i |AQ|+|QC|>|AC|
Dla nr 3
|AQ|+|QC|>|AC| i |DQ|+|QB|>|DB|
Widzę że w każdej tej możliwości
|AQ|+|QC|+|DQ|+|QB|>|AP|+|PB|+|CP|+|DP|
Więc punkt P jest tym jedynym punktem który spełnia warunki zadania .
I to by mi się zgadzało z rozwiązaniem i to jest prawidłowe rozumowanie jakie chciał autor
zadania .
Jednak autor zadaje dodatkowe pytanie . Czy potrafisz wskazać gdzie skorzystałeś z tego ze
czworokąt jest wypukły ?
A jakie to ma znaczenie czy jest wypukły czy wklęsły bo naprawdę nie wiem ?
Znajdz taki punkt wewnątrz danego czworokąta wypukłego aby suma odległości od wierzchołków
czworokąta była najmniejsza
Punkt P przecięcia sie przekątnych czworokąta ABCD będzie tym punktem wewnątrz danego
czworokąta dla którego suma odległości od wierzchołków czworokąta bedzie najmniejsza
Obieram sobie inny punkt Q który leże wewnątrz czworokąta
Musze udowodnić że
|AP|+DP|+|PC|+|PB|<|AQ|+DQ|+|CQ|+|BQ|
Mam że |AP|+|PC|+DP|+|PB|=|AC|+|DP| czyli długości obu przekątnych
Jesli P≠Q to mam 3 możliwości
1) Q∊AC
2) Q∊BD
3) Q∉AC i także Q∉BD
Dla nr 1
|AQ|+|QC|=|AC| i |BQ|+|QD|>|BD|
Dla nr 2
|DQ|+|QB|=|DB| i |AQ|+|QC|>|AC|
Dla nr 3
|AQ|+|QC|>|AC| i |DQ|+|QB|>|DB|
Widzę że w każdej tej możliwości
|AQ|+|QC|+|DQ|+|QB|>|AP|+|PB|+|CP|+|DP|
Więc punkt P jest tym jedynym punktem który spełnia warunki zadania .
I to by mi się zgadzało z rozwiązaniem i to jest prawidłowe rozumowanie jakie chciał autor
zadania .
Jednak autor zadaje dodatkowe pytanie . Czy potrafisz wskazać gdzie skorzystałeś z tego ze
czworokąt jest wypukły ?
A jakie to ma znaczenie czy jest wypukły czy wklęsły bo naprawdę nie wiem ?
