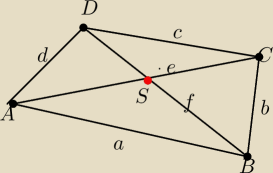
 Wykaż że w czworokącie wypukłym suma długości dwóch boków przeciwległych jest mniejsza od sumy
długości przekątnych
Mamy wykazac że
|AB|+|CD|<AC+|BD|
lub
|AD|+|BC|<|AC|+|DB|
S− punkt przecięcia sie przekątnych czworokąta
|AB|<|AS|+|SB|
|CD|<|DS|+|SC|
|AB|+|CD|<|AS|+|SC|+|DS|+|SB|
|AS|+SC|=|AC|
|DS|+|SB|=|DB|
|AB|+|CD|<|AC|+|DB|
|AD<|AS|+|SD|
|BC|<|BS|+|SC|
|AD|+|BC|<|AC|+|BD|
Wykaż że w czworokącie wypukłym suma długości dwóch boków przeciwległych jest mniejsza od sumy
długości przekątnych
Mamy wykazac że
|AB|+|CD|<AC+|BD|
lub
|AD|+|BC|<|AC|+|DB|
S− punkt przecięcia sie przekątnych czworokąta
|AB|<|AS|+|SB|
|CD|<|DS|+|SC|
|AB|+|CD|<|AS|+|SC|+|DS|+|SB|
|AS|+SC|=|AC|
|DS|+|SB|=|DB|
|AB|+|CD|<|AC|+|DB|
|AD<|AS|+|SD|
|BC|<|BS|+|SC|
|AD|+|BC|<|AC|+|BD|
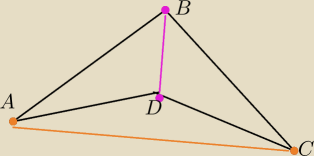 Mamy czworokąt niewypuky(wklęsły) ABCD
Przekątna to odcinek łączący dwa sąsiednie punkty które nie leżą na jednej prostej
Więc przekątne w tym wielokącie to BD i AC .
Jak zabrać sie za takie zadanie dla takiego czworokąta ?
Myślę że nie da rady bo które to miałyby byc boki przeciwległe . Nie ma
Mamy czworokąt niewypuky(wklęsły) ABCD
Przekątna to odcinek łączący dwa sąsiednie punkty które nie leżą na jednej prostej
Więc przekątne w tym wielokącie to BD i AC .
Jak zabrać sie za takie zadanie dla takiego czworokąta ?
Myślę że nie da rady bo które to miałyby byc boki przeciwległe . Nie ma