proszę o reozwiązanie anna: podstawą ostrosłupa prawidłowego trójkątnego ABCS jest trójkąt ABC Wysokość SD ma długość 12 i tworzy z krawędzią boczną kąt którego tangens jest równy 1/2 Oblicz pole powierzchni całkowitej tego ostrosłupa

Krzysiek: W podstawie takiego tójkata jest trójkąt równoboczny i sciany to trójkaty równoramienne Pytanie do Ciebie jest takie Gdzie w takim ostrosłupie (jesli w podstawie jest wielokąt foremny ) a trójkąt równoboczny jest takim wielokątem pada wysokośc ostrosłupa ?

wredulus_pospolitus: Krzysiek −−− przeczytaj na spokojnie to co napisałeś ... i popraw

Krzysiek: Tak zauważyłem W podstawie takiego ostrosłupa jest itd Zauważyłem ale nie chciało mi się poprawić . Lenistwo mnie ogarnia coraz bardziej Może przesilenie jesienne

anna: dla mnie ta treść jest niezrozumiała mam pytanie czy SD ta wysokość ma spodek w przecięciu się wysokości podstawy czy punkt D jest w połowie boku AB i to jest wysokość ostrosłupa

chichi: słabo doprecyzowane polecenie, ale gdyby mówiono o wysokości ściany bocznej, to pewnie by to zaznaczono. tutaj uznano, że mówiąc wysokość każdy pomyśli o wysokości ostrosłupa

Krzysiek: To pierwsze To drugie to wysokość sciany bocznej ostrosłupa

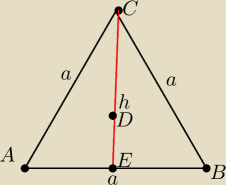
Krzysiek: CE =h− to wysokośc podstawy (czyli trójkata rownobocznego Wyskośc ostrosłupa− H pada pod kątem prostym na podstawe w punkcie D Punkt D jest srodkiem okręgu opisanego na tym trójkącie Ile wynosi długośc odcinka CD?

aaa:

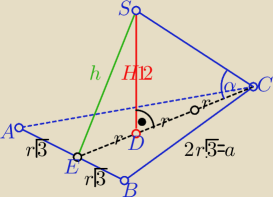
	12		1
tgα=		=		⇒ r=12 to h= 12√2
	2r		2

P_p= 3r²√3= .......... P_b= 3* r√3*h =........... Pc=.....

Krzysiek: Dobry wieczór Kąt α ma być między krawędzią boczna a wysokością ostrosłupa a nie wysokością podstawy

anna: wynik tego zadania to P_c = 432(√3 + √6) czy ktoś rozwiązał

anna: czy to nie jest kąt DSC ( kąt między wysokością a krawędzią boczną )

aaa: No tak czytanie ze zrozumienim się kłania (sorry) w takim razie

	2r		1
tgα=		=		⇒ r= 3
	12		2

teraz dokończ........

anna: P_c = 12 (√3 + √126) to chyba poprawne dziękuję

Krzysiek: Mi wyszedł inny wynik ale mogłem sie pomylic bo liczyłem w pamięci Napisz ile Ci wyszło pole podstawy i pole jednej powierzchni bocznej

chichi: √126 = 3√14

Krzysiek: Wysokośc podstawy h=9 stad obliczylem bok (a) podstawy

a√3
	=9
2

	18
a=		= 6√3
	√3

	a2√3		108√3
Pp=		=		= 27√3
	4		4

Wysokość (h_b) ściany bocznej (rysunek z 21:13 h_b²= H²+r² r=3 i H=12 h_b²=153 h_b=√153= √9*17=3√17 Pole jednej powierzchni bocznej P_pb P_pb= 0,5*a*h_b P_pb= 3√3*3√17= 9√51 Pole całkowite P_c P_c= P_p+3*P_pb P_c= 27√3+27√51= 27(√3+√51 Chyba sie nie pomylilem

anna: dziękuję bardzo